ML Theory Summary

Introduction

对概率的诠释有两大学派，一种是频率派另一种是贝叶斯派。后面我们对观测集采用下面记号：
\[ X_{N\times p}=(x_{1},x_{2},\cdots,x_{N})^{T},x_{i}=(x_{i1},x_{i2},\cdots,x_{ip})^{T} \]
这个记号表示有 \(N\) 个样本，每个样本都是 \(p\) 维向量。其中每个观测都是由 \(p(x|\theta)\) 生成的。

频率派的观点

\(p(x|\theta)\)中的 \(\theta\) 是一个常量。对于 \(N\) 个观测来说观测集的概率为 \(p(X|\theta)\mathop{=}\limits _{iid}\prod\limits _{i=1}^{N}p(x_{i}|\theta))\) 。为了求 \(\theta\) 的大小，我们采用最大对数似然MLE的方法：

\[ \theta_{MLE}=\mathop{argmax}\limits _{\theta}\log p(X|\theta)\mathop{=}\limits _{iid}\mathop{argmax}\limits _{\theta}\sum\limits _{i=1}^{N}\log p(x_{i}|\theta) \]

贝叶斯派的观点

贝叶斯派认为 \(p(x|\theta)\) 中的 \(\theta\) 不是一个常量。这个 \(\theta\) 满足一个预设的先验的分布 \(\theta\sim p(\theta)\) 。于是根据贝叶斯定理依赖观测集参数的后验可以写成：

\[ p(\theta|X)=\frac{p(X|\theta)\cdot p(\theta)}{p(X)}=\frac{p(X|\theta)\cdot p(\theta)}{\int\limits _{\theta}p(X|\theta)\cdot p(\theta)d\theta} \]
为了求 \(\theta\) 的值，我们要最大化这个参数后验MAP：

\[ \theta_{MAP}=\mathop{argmax}\limits _{\theta}p(\theta|X)=\mathop{argmax}\limits _{\theta}p(X|\theta)\cdot p(\theta) \]
其中第二个等号是由于分母和 \(\theta\) 没有关系。求解这个 \(\theta\) 值后计算\(\frac{p(X|\theta)\cdot p(\theta)}{\int\limits _{\theta}p(X|\theta)\cdot p(\theta)d\theta}\) ，就得到了参数的后验概率。其中 \(p(X|\theta)\) 叫似然，是我们的模型分布。得到了参数的后验分布后，我们可以将这个分布用于预测贝叶斯预测：
\[ p(x_{new}|X)=\int\limits _{\theta}p(x_{new}|\theta)\cdot p(\theta|X)d\theta \]
其中积分中的被乘数是模型，乘数是后验分布。

小结

频率派和贝叶斯派分别给出了一系列的机器学习算法。频率派的观点导出了一系列的统计机器学习算法而贝叶斯派导出了概率图理论。在应用频率派的 MLE 方法时最优化理论占有重要地位。而贝叶斯派的算法无论是后验概率的建模还是应用这个后验进行推断时积分占有重要地位。因此采样积分方法如 MCMC 有很多应用。

MathBasics

高斯分布

一维情况 MLE

高斯分布在机器学习中占有举足轻重的作用。在 MLE 方法中：

\[ \theta=(\mu,\Sigma)=(\mu,\sigma^{2}),\theta_{MLE}=\mathop{argmax}\limits _{\theta}\log p(X|\theta)\mathop{=}\limits _{iid}\mathop{argmax}\limits _{\theta}\sum\limits _{i=1}^{N}\log p(x_{i}|\theta) \]
一般地，高斯分布的概率密度函数PDF写为：

\[ p(x|\mu,\Sigma)=\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}e^{-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu)} \]
带入 MLE 中我们考虑一维的情况

\[ \log p(X|\theta)=\sum\limits _{i=1}^{N}\log p(x_{i}|\theta)=\sum\limits _{i=1}^{N}\log\frac{1}{\sqrt{2\pi}\sigma}\exp(-(x_{i}-\mu)^{2}/2\sigma^{2}) \]
首先对 \(\mu\) 的极值可以得到 ：
\[ \mu_{MLE}=\mathop{argmax}\limits _{\mu}\log p(X|\theta)=\mathop{argmax}\limits _{\mu}\sum\limits _{i=1}^{N}(x_{i}-\mu)^{2} \]
于是：
\[ \frac{\partial}{\partial\mu}\sum\limits _{i=1}^{N}(x_{i}-\mu)^{2}=0\longrightarrow\mu_{MLE}=\frac{1}{N}\sum\limits _{i=1}^{N}x_{i} \]
其次对 \(\theta\) 中的另一个参数 \(\sigma\) ，有：
\[ \begin{align*} \sigma_{MLE}=\mathop{argmax}\limits _{\sigma}\log p(X|\theta)&=\mathop{argmax}\limits _{\sigma}\sum\limits _{i=1}^{N}[-\log\sigma-\frac{1}{2\sigma^{2}}(x_{i}-\mu)^{2}]\\ &=\mathop{argmin}\limits _{\sigma}\sum\limits _{i=1}^{N}[\log\sigma+\frac{1}{2\sigma^{2}}(x_{i}-\mu)^{2}] \end{align*} \]
于是：
\[ \frac{\partial}{\partial\sigma}\sum\limits _{i=1}^{N}[\log\sigma+\frac{1}{2\sigma^{2}}(x_{i}-\mu)^{2}]=0\longrightarrow\sigma_{MLE}^{2}=\frac{1}{N}\sum\limits _{i=1}^{N}(x_{i}-\mu)^{2} \]
值得注意的是，上面的推导中，首先对 \(\mu\) 求 MLE， 然后利用这个结果求 \(\sigma_{MLE}\) ，因此可以预期的是对数据集求期望时 \(\mathbb{E}_{\mathcal{D}}[\mu_{MLE}]\) 是无偏差的：
\[ \mathbb{E}_{\mathcal{D}}[\mu_{MLE}]=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}]=\frac{1}{N}\sum\limits _{i=1}^{N}\mathbb{E}_{\mathcal{D}}[x_{i}]=\mu \]
但是当对 \(\sigma_{MLE}\) 求 期望的时候由于使用了单个数据集的 \(\mu_{MLE}\)，因此对所有数据集求期望的时候我们会发现 \(\sigma_{MLE}\) 是 有偏的：

\[ \begin{align*} \mathbb{E}_{\mathcal{D}}[\sigma_{MLE}^{2}]&=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}(x_{i}-\mu_{MLE})^{2}]=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}(x_{i}^{2}-2x_{i}\mu_{MLE}+\mu_{MLE}^{2}) \\&=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}^{2}-\mu_{MLE}^{2}]=\mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}^{2}-\mu^{2}+\mu^{2}-\mu_{MLE}^{2}]\\ &= \mathbb{E}_{\mathcal{D}}[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}^{2}-\mu^{2}]-\mathbb{E}_{\mathcal{D}}[\mu_{MLE}^{2}-\mu^{2}]=\sigma^{2}-(\mathbb{E}_{\mathcal{D}}[\mu_{MLE}^{2}]-\mu^{2})r\\&=\sigma^{2}-(\mathbb{E}_{\mathcal{D}}[\mu_{MLE}^{2}]-\mathbb{E}_{\mathcal{D}}^{2}[\mu_{MLE}])=\sigma^{2}-Var[\mu_{MLE}]\\&=\sigma^{2}-Var[\frac{1}{N}\sum\limits _{i=1}^{N}x_{i}]=\sigma^{2}-\frac{1}{N^{2}}\sum\limits _{i=1}^{N}Var[x_{i}]=\frac{N-1}{N}\sigma^{2} \end{align*} \]
所以：
\[ \hat{\sigma}^{2}=\frac{1}{N-1}\sum\limits _{i=1}^{N}(x_{i}-\mu)^{2} \]

多维情况

多维高斯分布表达式为：
\[ p(x|\mu,\Sigma)=\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}e^{-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu)} \]
其中 \(x,\mu\in\mathbb{R}^{p},\Sigma\in\mathbb{R}^{p\times p}\) ，\(\Sigma\) 为协方差矩阵，一般而言也是半正定矩阵。这里我们只考虑正定矩阵。首先我们处理指数上的数字，指数上的数字可以记为 \(x\) 和 \(\mu\) 之间的马氏距离。对于对称的协方差矩阵可进行特征值分解，\(\Sigma=U\Lambda U^{T}=(u_{1},u_{2},\cdots,u_{p})diag(\lambda_{i})(u_{1},u_{2},\cdots,u_{p})^{T}=\sum\limits _{i=1}^{p}u_{i}\lambda_{i}u_{i}^{T}\) ，于是：

\[ \Sigma^{-1}=\sum\limits _{i=1}^{p}u_{i}\frac{1}{\lambda_{i}}u_{i}^{T} \]

\[ \Delta=(x-\mu)^{T}\Sigma^{-1}(x-\mu)=\sum\limits _{i=1}^{p}(x-\mu)^{T}u_{i}\frac{1}{\lambda_{i}}u_{i}^{T}(x-\mu)=\sum\limits _{i=1}^{p}\frac{y_{i}^{2}}{\lambda_{i}} \]

我们注意到 \(y_{i}\) 是 \(x-\mu\) 在特征向量 \(u_{i}\) 上的投影长度，因此上式子就是 \(\Delta\) 取不同值时的同心椭圆。

下面我们看多维高斯模型在实际应用时的两个问题

1. 参数 \(\Sigma,\mu\) 的自由度为 \(O(p^{2})\) 对于维度很高的数据其自由度太高。解决方案：高自由度的来源是 \(\Sigma\) 有 \(\frac{p(p+1)}{2}\) 个自由参数，可以假设其是对角矩阵，甚至在各向同性假设中假设其对角线上的元素都相同。前一种的算法有 Factor Analysis，后一种有概率 PCA(p-PCA) 。

2. 第二个问题是单个高斯分布是单峰的，对有多个峰的数据分布不能得到好的结果。解决方案：高斯混合GMM 模型。

下面对多维高斯分布的常用定理进行介绍。

我们记 \(x=(x_1, x_2,\cdots,x_p)^T=(x_{a,m\times 1}, x_{b,n\times1})^T,\mu=(\mu_{a,m\times1}, \mu_{b,n\times1}),\Sigma=\begin{pmatrix}\Sigma_{aa}&\Sigma_{ab}\\\Sigma_{ba}&\Sigma_{bb}\end{pmatrix}\)，已知 \(x\sim\mathcal{N}(\mu,\Sigma)\)。

首先是一个高斯分布的定理：

定理：已知 \(x\sim\mathcal{N}(\mu,\Sigma), y\sim Ax+b\)，那么 \(y\sim\mathcal{N}(A\mu+b, A\Sigma A^T)\)。

证明：\(\mathbb{E}[y]=\mathbb{E}[Ax+b]=A\mathbb{E}[x]+b=A\mu+b\)，\(Var[y]=Var[Ax+b]=Var[Ax]=A\cdot Var[x]\cdot A^T\)。

下面利用这个定理得到 \(p(x_a),p(x_b),p(x_a|x_b),p(x_b|x_a)\) 这四个量。

1. \(x_a=\begin{pmatrix}\mathbb{I}_{m\times m}&\mathbb{O}_{m\times n})\end{pmatrix}\begin{pmatrix}x_a\\x_b\end{pmatrix}\)，代入定理中得到：
   \[ \mathbb{E}[x_a]=\begin{pmatrix}\mathbb{I}&\mathbb{O}\end{pmatrix}\begin{pmatrix}\mu_a\\\mu_b\end{pmatrix}=\mu_a\\ Var[x_a]=\begin{pmatrix}\mathbb{I}&\mathbb{O}\end{pmatrix}\begin{pmatrix}\Sigma_{aa}&\Sigma_{ab}\\\Sigma_{ba}&\Sigma_{bb}\end{pmatrix}\begin{pmatrix}\mathbb{I}\\\mathbb{O}\end{pmatrix}=\Sigma_{aa} \]
   所以 \(x_a\sim\mathcal{N}(\mu_a,\Sigma_{aa})\)。

2. 同样的，\(x_b\sim\mathcal{N}(\mu_b,\Sigma_{bb})\)。

3. 对于两个条件概率，我们引入三个量：
   \[ \begin{gather*} x_{b\cdot a}=x_b-\Sigma_{ba}\Sigma_{aa}^{-1}x_a\\ \mu_{b\cdot a}=\mu_b-\Sigma_{ba}\Sigma_{aa}^{-1}\mu_a\\ \Sigma_{bb\cdot a}=\Sigma_{bb}-\Sigma_{ba}\Sigma_{aa}^{-1}\Sigma_{ab} \end{gather*} \]
   特别的，最后一个式子叫做 \(\Sigma_{bb}\) 的 Schur Complementary。可以看到：
   \[ x_{b\cdot a}=\begin{pmatrix}-\Sigma_{ba}\Sigma_{aa}^{-1}&\mathbb{I}_{n\times n}\end{pmatrix}\begin{pmatrix}x_a\\x_b\end{pmatrix} \]
   所以：
   \[ \begin{gather*} \mathbb{E}[x_{b\cdot a}]=\begin{pmatrix}-\Sigma_{ba}\Sigma_{aa}^{-1}&\mathbb{I}_{n\times n}\end{pmatrix}\begin{pmatrix}\mu_a\\\mu_b\end{pmatrix}=\mu_{b\cdot a}\\ Var[x_{b\cdot a}]=\begin{pmatrix}-\Sigma_{ba}\Sigma_{aa}^{-1}&\mathbb{I}_{n\times n}\end{pmatrix}\begin{pmatrix}\Sigma_{aa}&\Sigma_{ab}\\\Sigma_{ba}&\Sigma_{bb}\end{pmatrix}\begin{pmatrix}-\Sigma_{aa}^{-1}\Sigma_{ba}^T\\\mathbb{I}_{n\times n}\end{pmatrix}=\Sigma_{bb\cdot a} \end{gather*} \]
   利用这三个量可以得到 \(x_b=x_{b\cdot a}+\Sigma_{ba}\Sigma_{aa}^{-1}x_a\)。因此：
   \[ \begin{gather*} \mathbb{E}[x_b|x_a]=\mu_{b\cdot a}+\Sigma_{ba}\Sigma_{aa}^{-1}x_a\\ Var[x_b|x_a]=\Sigma_{bb\cdot a} \end{gather*} \]

   这里同样用到了定理。

4. 同样：
   \[ \begin{gather*} x_{a\cdot b}=x_a-\Sigma_{ab}\Sigma_{bb}^{-1}x_b\\ \mu_{a\cdot b}=\mu_a-\Sigma_{ab}\Sigma_{bb}^{-1}\mu_b\\ \Sigma_{aa\cdot b}=\Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba} \end{gather*} \]
   所以：
   \[ \mathbb{E}[x_a|x_b]=\mu_{a\cdot b}+\Sigma_{ab}\Sigma_{bb}^{-1}x_b \]

   \[ Var[x_a|x_b]=\Sigma_{aa\cdot b} \]

下面利用上边四个量，求解线性模型：

已知：\(p(x)=\mathcal{N}(\mu,\Lambda^{-1}),p(y|x)=\mathcal{N}(Ax+b,L^{-1})\)，求解：\(p(y),p(x|y)\)。

解：令 \(y=Ax+b+\epsilon,\epsilon\sim\mathcal{N}(0,L^{-1})\)，所以 \(\mathbb{E}[y]=\mathbb{E}[Ax+b+\epsilon]=A\mu+b\)，\(Var[y]=A \Lambda^{-1}A^T+L^{-1}\)，因此：
\[ p(y)=\mathcal{N}(A\mu+b,L^{-1}+A\Lambda^{-1}A^T) \]
引入 \(z=\begin{pmatrix}x\\y\end{pmatrix}\)，我们可以得到 \(Cov[x,y]=\mathbb{E}[(x-\mathbb{E}[x])(y-\mathbb{E}[y])^T]\)。对于这个协方差可以直接计算：
\[ \begin{align*} Cov(x,y)&=\mathbb{E}[(x-\mu)(Ax-A\mu+\epsilon)^T]=\mathbb{E}[(x-\mu)(x-\mu)^TA^T]=Var[x]A^T=\Lambda^{-1}A^T \end{align*} \]
注意到协方差矩阵的对称性，所以 \(p(z)=\mathcal{N}\begin{pmatrix}\mu\\A\mu+b\end{pmatrix},\begin{pmatrix}\Lambda^{-1}&\Lambda^{-1}A^T\\A\Lambda^{-1}&L^{-1}+A\Lambda^{-1}A^T\end{pmatrix})\)。根据之前的公式，我们可以得到：
\[ \mathbb{E}[x|y]=\mu+\Lambda^{-1}A^T(L^{-1}+A\Lambda^{-1}A^T)^{-1}(y-A\mu-b) \]

\[ Var[x|y]=\Lambda^{-1}-\Lambda^{-1}A^T(L^{-1}+A\Lambda^{-1}A^T)^{-1}A\Lambda^{-1} \]

线性回归

假设数据集为：
\[ \mathcal{D}=\{(x_1, y_1),(x_2, y_2),\cdots,(x_N, y_N)\} \]
后面我们记：
\[ X=(x_1,x_2,\cdots,x_N)^T,Y=(y_1,y_2,\cdots,y_N)^T \]
线性回归假设：
\[ f(w)=w^Tx \]

最小二乘法

对这个问题，采用二范数定义的平方误差来定义损失函数：
\[ L(w)=\sum\limits_{i=1}^N||w^Tx_i-y_i||^2_2 \]
展开得到：
\[ \begin{align*} L(w)&=(w^Tx_1-y_1,\cdots,w^Tx_N-y_N)\cdot (w^Tx_1-y_1,\cdots,w^Tx_N-y_N)^T\\ &=(w^TX^T-Y^T)\cdot (Xw-Y)=w^TX^TXw-Y^TXw-w^TX^TY+Y^TY\\ &=w^TX^TXw-2w^TX^TY+Y^TY \end{align*} \]
最小化这个值的 $ $ ：
\[ \begin{align*} \hat{w}=\mathop{argmin}\limits_wL(w)&\longrightarrow\frac{\partial}{\partial w}L(w)=0\\ &\longrightarrow2X^TX\hat{w}-2X^TY=0\\ &\longrightarrow \hat{w}=(X^TX)^{-1}X^TY=X^+Y \end{align*} \]
这个式子中 \((X^TX)^{-1}X^T\) 又被称为伪逆。对于行满秩或者列满秩的 \(X\)，可以直接求解，但是对于非满秩的样本集合，需要使用奇异值分解（SVD）的方法，对 \(X\) 求奇异值分解，得到
\[ X=U\Sigma V^T \]
于是：
\[ X^+=V\Sigma^{-1}U^T \]
在几何上，最小二乘法相当于模型（这里就是直线）和试验值的距离的平方求和，假设我们的试验样本张成一个 \(p\) 维空间（满秩的情况）：\(X=Span(x_1,\cdots,x_N)\)，而模型可以写成 \(f(w)=X\beta\)，也就是 \(x_1,\cdots,x_N\) 的某种组合，而最小二乘法就是说希望 \(Y\) 和这个模型距离越小越好，于是它们的差应该与这个张成的空间垂直：
\[ X^T\cdot(Y-X\beta)=0\longrightarrow\beta=(X^TX)^{-1}X^TY \]

噪声为高斯分布的 MLE

对于一维的情况，记 \(y=w^Tx+\epsilon,\epsilon\sim\mathcal{N}(0,\sigma^2)\)，那么 \(y\sim\mathcal{N}(w^Tx,\sigma^2)\)。代入极大似然估计中：
\[ \begin{align*} L(w)=\log p(Y|X,w)&=\log\prod\limits_{i=1}^Np(y_i|x_i,w)\\ &=\sum\limits_{i=1}^N\log(\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{(y_i-w^Tx_i)^2}{2\sigma^2}})\\ \mathop{argmax}\limits_wL(w)&=\mathop{argmin}\limits_w\sum\limits_{i=1^N}(y_i-w^Tx_i)^2 \end{align*} \]
这个表达式和最小二乘估计得到的结果一样。

权重先验也为高斯分布的 MAP

取先验分布 \(w\sim\mathcal{N}(0,\sigma_0^2)\)。于是： 
\[ \begin{align*} \hat{w}=\mathop{argmax}\limits_wp(w|Y)&=\mathop{argmax}\limits_wp(Y|w)p(w)\\ &=\mathop{argmax}\limits_w\log p(Y|w)p(w)\\ &=\mathop{argmax}\limits_w(\log p(Y|w)+\log p(w))\\ &=\mathop{argmin}\limits_w[(y-w^Tx)^2+\frac{\sigma^2}{\sigma_0^2}w^Tw] \end{align*} \]
这里省略了 \(X\)，\(p(Y)\)和 \(w\) 没有关系，同时也利用了上面高斯分布的 MLE的结果。

我们将会看到，超参数 \(\sigma_0\)的存在和下面会介绍的 Ridge 正则项可以对应，同样的如果将先验分布取为 Laplace 分布，那么就会得到和 L1 正则类似的结果。

正则化

在实际应用时，如果样本容量不远远大于样本的特征维度，很可能造成过拟合，对这种情况，我们有下面三个解决方式：

1. 加数据
2. 特征选择（降低特征维度）如 PCA 算法。
3. 正则化

正则化一般是在损失函数（如上面介绍的最小二乘损失）上加入正则化项（表示模型的复杂度对模型的惩罚），下面我们介绍一般情况下的两种正则化框架。
\[ \begin{align*} L1&:\mathop{argmin}\limits_wL(w)+\lambda||w||_1,\lambda\gt0\\ L2&:\mathop{argmin}\limits_wL(w)+\lambda||w||^2_2,\lambda \gt 0 \end{align*} \]
下面对最小二乘误差分别分析这两者的区别。

L1 Lasso

L1正则化可以引起稀疏解。

从最小化损失的角度看，由于 L1 项求导在0附近的左右导数都不是0，因此更容易取到0解。

从另一个方面看，L1 正则化相当于：
\[ \begin{gather*} \mathop{argmin}\limits_wL(w)\\ s.t. ||w||_1\lt C \end{gather*} \]
我们已经看到平方误差损失函数在 \(w\) 空间是一个椭球，因此上式求解就是椭球和 \(||w||_1=C\)的切点，因此更容易相切在坐标轴上。

L2 Ridge

\[ \begin{align*} \hat{w}=\mathop{argmin}\limits_wL(w)+\lambda w^Tw&\longrightarrow\frac{\partial}{\partial w}L(w)+2\lambda w=0\\ &\longrightarrow2X^TX\hat{w}-2X^TY+2\lambda \hat w=0\\ &\longrightarrow \hat{w}=(X^TX+\lambda \mathbb{I})^{-1}X^TY \end{align*} \]

可以看到，这个正则化参数和前面的 MAP 结果不谋而合。利用2范数进行正则化不仅可以是模型选择 \(w\) 较小的参数，同时也避免 $ X^TX$不可逆的问题。

小结

线性回归模型是最简单的模型，但是麻雀虽小，五脏俱全，在这里，我们利用最小二乘误差得到了闭式解。同时也发现，在噪声为高斯分布的时候，MLE 的解等价于最小二乘误差，而增加了正则项后，最小二乘误差加上 L2 正则项等价于高斯噪声先验下的 MAP解，加上 L1 正则项后，等价于 Laplace 噪声先验。

传统的机器学习方法或多或少都有线性回归模型的影子：

1. 线性模型往往不能很好地拟合数据，因此有三种方案克服这一劣势：
   1. 对特征的维数进行变换，例如多项式回归模型就是在线性特征的基础上加入高次项。
   2. 在线性方程后面加入一个非线性变换，即引入一个非线性的激活函数，典型的有线性分类模型如感知机。
   3. 对于一致的线性系数，我们进行多次变换，这样同一个特征不仅仅被单个系数影响，例如多层感知机（深度前馈网络）。
2. 线性回归在整个样本空间都是线性的，我们修改这个限制，在不同区域引入不同的线性或非线性，例如线性样条回归和决策树模型。
3. 线性回归中使用了所有的样本，但是对数据预先进行加工学习的效果可能更好（所谓的维数灾难，高维度数据更难学习），例如 PCA 算法和流形学习。

线性分类

对于分类任务，线性回归模型就无能为力了，但是我们可以在线性模型的函数进行后再加入一层激活函数，这个函数是非线性的，激活函数的反函数叫做链接函数。我们有两种线性分类的方式：

1. 硬分类，我们直接需要输出观测对应的分类。这类模型的代表为：
   1. 线性判别分析（Fisher 判别）
   2. 感知机
2. 软分类，产生不同类别的概率，这类算法根据概率方法的不同分为两种
   1. 生成式（根据贝叶斯定理先计算参数后验，再进行推断）：高斯判别分析（GDA）和朴素贝叶斯等为代表
      1. GDA
      2. Naive Bayes
   2. 判别式（直接对条件概率进行建模）：Logistic 回归

两分类-硬分类-感知机算法

我们选取激活函数为：
\[ sign(a)=\left\{\begin{matrix}+1,a\ge0\\-1,a\lt0\end{matrix}\right. \]
这样就可以将线性回归的结果映射到两分类的结果上了。

定义损失函数为错误分类的数目，比较直观的方式是使用指示函数，但是指示函数不可导，因此可以定义：
\[ L(w)=\sum\limits_{x_i\in\mathcal{D}_{wrong}}-y_iw^Tx_i \]
其中，\(\mathcal{D}_{wrong}\)是错误分类集合，实际在每一次训练的时候，我们采用梯度下降的算法。损失函数对 \(w\) 的偏导为：
\[ \frac{\partial}{\partial w}L(w)=\sum\limits_{x_i\in\mathcal{D}_{wrong}}-y_ix_i \]
但是如果样本非常多的情况下，计算复杂度较高，但是，实际上我们并不需要绝对的损失函数下降的方向，我们只需要损失函数的期望值下降，但是计算期望需要知道真实的概率分布，我们实际只能根据训练数据抽样来估算这个概率分布（经验风险）：
\[ \mathbb{E}_{\mathcal D}[\mathbb{E}_\hat{p}[\nabla_wL(w)]]=\mathbb{E}_{\mathcal D}[\frac{1}{N}\sum\limits_{i=1}^N\nabla_wL(w)] \]
我们知道， \(N\) 越大，样本近似真实分布越准确，但是对于一个标准差为 \(\sigma\) 的数据，可以确定的标准差仅和 \(\sqrt{N}\) 成反比，而计算速度却和 \(N\) 成正比。因此可以每次使用较少样本，则在数学期望的意义上损失降低的同时，有可以提高计算速度，如果每次只使用一个错误样本，我们有下面的更新策略（根据泰勒公式，在负方向）：
\[ w^{t+1}\leftarrow w^{t}+\lambda y_ix_i \]
是可以收敛的，同时使用单个观测更新也可以在一定程度上增加不确定度，从而减轻陷入局部最小的可能。在更大规模的数据上，常用的是小批量随机梯度下降法。

两分类-硬分类-线性判别分析 LDA

在 LDA 中，我们的基本想法是选定一个方向，将试验样本顺着这个方向投影，投影后的数据需要满足两个条件，从而可以更好地分类：

1. 相同类内部的试验样本距离接近。
2. 不同类别之间的距离较大。

首先是投影，我们假定原来的数据是向量 \(x\)，那么顺着 $ w$ 方向的投影就是标量：
\[ z=w^T\cdot x(=|w|\cdot|x|\cos\theta) \]
对第一点，相同类内部的样本更为接近，我们假设属于两类的试验样本数量分别是 \(N_1\)和 \(N_2\)，那么我们采用方差矩阵来表征每一个类内的总体分布，这里我们使用了协方差的定义，用 \(S\) 表示原数据的协方差：
\[ \begin{align*} C_1:Var_z[C_1]&=\frac{1}{N_1}\sum\limits_{i=1}^{N_1}(z_i-\overline{z_{c1}})(z_i-\overline{z_{c1}})^T\\ &=\frac{1}{N_1}\sum\limits_{i=1}^{N_1}(w^Tx_i-\frac{1}{N_1}\sum\limits_{j=1}^{N_1}w^Tx_j)(w^Tx_i-\frac{1}{N_1}\sum\limits_{j=1}^{N_1}w^Tx_j)^T\\ &=w^T\frac{1}{N_1}\sum\limits_{i=1}^{N_1}(x_i-\overline{x_{c1}})(x_i-\overline{x_{c1}})^Tw\\ &=w^TS_1w\\ C_2:Var_z[C_2]&=\frac{1}{N_2}\sum\limits_{i=1}^{N_2}(z_i-\overline{z_{c2}})(z_i-\overline{z_{c2}})^T\\ &=w^TS_2w \end{align*} \]
所以类内距离可以记为：
\[ \begin{align*} Var_z[C_1]+Var_z[C_2]=w^T(S_1+S_2)w \end{align*} \]
对于第二点，我们可以用两类的均值表示这个距离：
\[ \begin{align*} (\overline{z_{c1}}-\overline{z_{c2}})^2&=(\frac{1}{N_1}\sum\limits_{i=1}^{N_1}w^Tx_i-\frac{1}{N_2}\sum\limits_{i=1}^{N_2}w^Tx_i)^2\\ &=(w^T(\overline{x_{c1}}-\overline{x_{c2}}))^2\\ &=w^T(\overline{x_{c1}}-\overline{x_{c2}})(\overline{x_{c1}}-\overline{x_{c2}})^Tw \end{align*} \]
综合这两点，由于协方差是一个矩阵，于是我们用将这两个值相除来得到我们的损失函数，并最大化这个值：
\[ \begin{align*} \hat{w}=\mathop{argmax}\limits_wJ(w)&=\mathop{argmax}\limits_w\frac{(\overline{z_{c1}}-\overline{z_{c2}})^2}{Var_z[C_1]+Var_z[C_2]}\\ &=\mathop{argmax}\limits_w\frac{w^T(\overline{x_{c1}}-\overline{x_{c2}})(\overline{x_{c1}}-\overline{x_{c2}})^Tw}{w^T(S_1+S_2)w}\\ &=\mathop{argmax}\limits_w\frac{w^TS_bw}{w^TS_ww} \end{align*} \]
这样，我们就把损失函数和原数据集以及参数结合起来了。下面对这个损失函数求偏导，注意我们其实对 \(w\) 的绝对值没有任何要求，只对方向有要求，因此只要一个方程就可以求解了：
\[ \begin{gather*} \frac{\partial}{\partial w}J(w)=2S_bw(w^TS_ww)^{-1}-2w^TS_bw(w^TS_ww)^{-2}S_ww=0\\ \Longrightarrow S_bw(w^TS_ww)=(w^TS_bw)S_ww\\ \Longrightarrow w\propto S_w^{-1}S_bw=S_w^{-1}(\overline{x_{c1}}-\overline{x_{c2}})(\overline{x_{c1}}-\overline{x_{c2}})^Tw\propto S_w^{-1}(\overline{x_{c1}}-\overline{x_{c2}}) \end{gather*} \]
于是 $ S_w^{-1}(-)$ 就是我们需要寻找的方向。最后可以归一化求得单位的 \(w\) 值。

两分类-软分类-概率判别模型-Logistic 回归

有时候我们只要得到一个类别的概率，那么我们需要一种能输出 \([0,1]\) 区间的值的函数。考虑两分类模型，我们利用判别模型，希望对 \(p(C|x)\) 建模，利用贝叶斯定理：
\[ p(C_1|x)=\frac{p(x|C_1)p(C_1)}{p(x|C_1)p(C_1)+p(x|C_2)p(C_2)} \]
取 \(a=\ln\frac{p(x|C_1)p(C_1)}{p(x|C_2)p(C_2)}\)，于是：
\[ p(C_1|x)=\frac{1}{1+\exp(-a)} \]
上面的式子叫 Logistic Sigmoid 函数，其参数表示了两类联合概率比值的对数。在判别式中，不关心这个参数的具体值，模型假设直接对 \(a\) 进行。

Logistic 回归的模型假设是：
\[ a=w^Tx \]
于是，通过寻找 $  w$ 的最佳值可以得到在这个模型假设下的最佳模型。概率判别模型常用最大似然估计的方式来确定参数。

对于一次观测，获得分类 \(y\) 的概率为（假定\(C_1=1,C_2=0\)）：
\[ p(y|x)=p_1^yp_0^{1-y} \]

那么对于 \(N\) 次独立全同的观测 MLE为：
\[ \hat{w}=\mathop{argmax}_wJ(w)=\mathop{argmax}_w\sum\limits_{i=1}^N(y_i\log p_1+(1-y_i)\log p_0) \]
注意到，这个表达式是交叉熵表达式的相反数乘 \(N\)，MLE 中的对数也保证了可以和指数函数相匹配，从而在大的区间汇总获取稳定的梯度。

对这个函数求导数，注意到：
\[ p_1'=(\frac{1}{1+\exp(-a)})'=p_1(1-p_1) \]
则：
\[ J'(w)=\sum\limits_{i=1}^Ny_i(1-p_1)x_i-p_1x_i+y_ip_1x_i=\sum\limits_{i=1}^N(y_i-p_1)x_i \]
由于概率值的非线性，放在求和符号中时，这个式子无法直接求解。于是在实际训练的时候，和感知机类似，也可以使用不同大小的批量随机梯度上升（对于最小化就是梯度下降）来获得这个函数的极大值。

两分类-软分类-概率生成模型-高斯判别分析 GDA

生成模型中，我们对联合概率分布进行建模，然后采用 MAP 来获得参数的最佳值。两分类的情况，我们采用的假设：

1. \(y\sim Bernoulli(\phi)\)
2. \(x|y=1\sim\mathcal{N}(\mu_1,\Sigma)\)
3. \(x|y=0\sim\mathcal{N}(\mu_0,\Sigma)\)

那么独立全同的数据集最大后验概率可以表示为：
\[ \begin{align*} \mathop{argmax}_{\phi,\mu_0,\mu_1,\Sigma}\log p(X|Y)p(Y)=\mathop{argmax}_{\phi,\mu_0,\mu_1,\Sigma}\sum\limits_{i=1}^N (\log p(x_i|y_i)+\log p(y_i))\\ =\mathop{argmax}_{\phi,\mu_0,\mu_1,\Sigma}\sum\limits_{i=1}^N((1-y_i)\log\mathcal{N}(\mu_0,\Sigma)+y_i\log \mathcal{N}(\mu_1,\Sigma)+y_i\log\phi+(1-y_i)\log(1-\phi)) \end{align*} \]

• 首先对 \(\phi\) 进行求解，将式子对 \(\phi\) 求偏导：
  \[ \begin{align*}\sum\limits_{i=1}^N\frac{y_i}{\phi}+\frac{y_i-1}{1-\phi}=0\\ \Longrightarrow\phi=\frac{\sum\limits_{i=1}^Ny_i}{N}=\frac{N_1}{N} \end{align*} \]

• 然后求解 \(\mu_1\)：
  \[ \begin{align*}\hat{\mu_1}&=\mathop{argmax}_{\mu_1}\sum\limits_{i=1}^Ny_i\log\mathcal{N}(\mu_1,\Sigma)\\ &=\mathop{argmin}_{\mu_1}\sum\limits_{i=1}^Ny_i(x_i-\mu_1)^T\Sigma^{-1}(x_i-\mu_1) \end{align*} \]
  由于：
  \[ \sum\limits_{i=1}^Ny_i(x_i-\mu_1)^T\Sigma^{-1}(x_i-\mu_1)=\sum\limits_{i=1}^Ny_ix_i^T\Sigma^{-1}x_i-2y_i\mu_1^T\Sigma^{-1}x_i+y_i\mu_1^T\Sigma^{-1}\mu_1 \]

  求微分左边乘以 \(\Sigma\) 可以得到：
  \[ \begin{align*}\sum\limits_{i=1}^N-2y_i\Sigma^{-1}x_i+2y_i\Sigma^{-1}\mu_1=0\\ \Longrightarrow\mu_1=\frac{\sum\limits_{i=1}^Ny_ix_i}{\sum\limits_{i=1}^Ny_i}=\frac{\sum\limits_{i=1}^Ny_ix_i}{N_1} \end{align*} \]

• 求解 \(\mu_0\)，由于正反例是对称的，所以：
  \[ \mu_0=\frac{\sum\limits_{i=1}^N(1-y_i)x_i}{N_0} \]

• 最为困难的是求解 \(\Sigma\)，我们的模型假设对正反例采用相同的协方差矩阵，当然从上面的求解中我们可以看到，即使采用不同的矩阵也不会影响之前的三个参数。首先我们有：
  \[ \begin{align*} \sum\limits_{i=1}^N\log\mathcal{N}(\mu,\Sigma)&=\sum\limits_{i=1}^N\log(\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}})+(-\frac{1}{2}(x_i-\mu)^T\Sigma^{-1}(x_i-\mu))\\ &=Const-\frac{1}{2}N\log|\Sigma|-\frac{1}{2}Trace((x_i-\mu)^T\Sigma^{-1}(x_i-\mu))\\ &=Const-\frac{1}{2}N\log|\Sigma|-\frac{1}{2}Trace((x_i-\mu)(x_i-\mu)^T\Sigma^{-1})\\ &=Const-\frac{1}{2}N\log|\Sigma|-\frac{1}{2}NTrace(S\Sigma^{-1}) \end{align*} \]
  在这个表达式中，我们在标量上加入迹从而可以交换矩阵的顺序，对于包含绝对值和迹的表达式的导数，我们有：
  \[ \begin{align*} \frac{\partial}{\partial A}(|A|)&=|A|A^{-1}\\ \frac{\partial}{\partial A}Trace(AB)&=B^T \end{align*} \]
  因此：
  \[ \begin{align*}[\sum\limits_{i=1}^N((1-y_i)\log\mathcal{N}(\mu_0,\Sigma)+y_i\log \mathcal{N}(\mu_1,\Sigma)]' \\=Const-\frac{1}{2}N\log|\Sigma|-\frac{1}{2}N_1Trace(S_1\Sigma^{-1})-\frac{1}{2}N_2Trace(S_2\Sigma^{-1}) \end{align*} \]
  其中，\(S_1,S_2\) 分别为两个类数据内部的协方差矩阵，于是：
  \[ \begin{align*}N\Sigma^{-1}-N_1S_1^T\Sigma^{-2}-N_2S_2^T\Sigma^{-2}=0 \\\Longrightarrow\Sigma=\frac{N_1S_1+N_2S_2}{N} \end{align*} \]
  这里应用了类协方差矩阵的对称性。

于是我们就利用最大后验的方法求得了我们模型假设里面的所有参数，根据模型，可以得到联合分布，也就可以得到用于推断的条件分布了。

两分类-软分类-概率生成模型-朴素贝叶斯

上面的高斯判别分析的是对数据集的分布作出了高斯分布的假设，同时引入伯努利分布作为类先验，从而利用最大后验求得这些假设中的参数。

朴素贝叶斯队数据的属性之间的关系作出了假设，一般地，我们有需要得到 \(p(x|y)\) 这个概率值，由于 \(x\) 有 \(p\) 个维度，因此需要对这么多的维度的联合概率进行采样，但是我们知道这么高维度的空间中采样需要的样本数量非常大才能获得较为准确的概率近似。

在一般的有向概率图模型中，对各个属性维度之间的条件独立关系作出了不同的假设，其中最为简单的一个假设就是在朴素贝叶斯模型描述中的条件独立性假设。
\[ p(x|y)=\prod\limits_{i=1}^pp(x_i|y) \]
即：
\[ x_i\perp x_j|y,\forall\ i\ne j \]
于是利用贝叶斯定理，对于单次观测：
\[ p(y|x)=\frac{p(x|y)p(y)}{p(x)}=\frac{\prod\limits_{i=1}^pp(x_i|y)p(y)}{p(x)} \]
对于单个维度的条件概率以及类先验作出进一步的假设：

1. \(x_i\) 为连续变量：\(p(x_i|y)=\mathcal{N}(\mu_i,\sigma_i^2)\)
2. \(x_i\) 为离散变量：类别分布（Categorical）：\(p(x_i=i|y)=\theta_i,\sum\limits_{i=1}^K\theta_i=1\)
3. \(p(y)=\phi^y(1-\phi)^{1-y}\)

对这些参数的估计，常用 MLE 的方法直接在数据集上估计，由于不需要知道各个维度之间的关系，因此，所需数据量大大减少了。估算完这些参数，再代入贝叶斯定理中得到类别的后验分布。

小结

分类任务分为两类，对于需要直接输出类别的任务，感知机算法中我们在线性模型的基础上加入符号函数作为激活函数，那么就能得到这个类别，但是符号函数不光滑，于是我们采用错误驱动的方式，引入 \(\sum\limits_{x_i\in\mathcal{D}_{wrong}}-y_iw^Tx_i\) 作为损失函数，然后最小化这个误差，采用批量随机梯度下降的方法来获取最佳的参数值。而在线性判别分析中，我们将线性模型看作是数据点在某一个方向的投影，采用类内小，类间大的思路来定义损失函数，其中类内小定义为两类数据的方差之和，类间大定义为两类数据中心点的间距，对损失函数求导得到参数的方向，这个方向就是 \(S_w^{-1}(\overline x_{c1}-\overline x_{c2})\)，其中 \(S_w\) 为原数据集两类的方差之和。

另一种任务是输出分类的概率，对于概率模型，我们有两种方案，第一种是判别模型，也就是直接对类别的条件概率建模，将线性模型套入 Logistic 函数中，我们就得到了 Logistic 回归模型，这里的概率解释是两类的联合概率比值的对数是线性的，我们定义的损失函数是交叉熵（等价于 MLE），对这个函数求导得到 \(\frac{1}{N}\sum\limits_{i=1}^N(y_i-p_1)x_i\)，同样利用批量随机梯度（上升）的方法进行优化。第二种是生成模型，生成模型引入了类别的先验，在高斯判别分析中，我们对数据集的数据分布作出了假设，其中类先验是二项分布，而每一类的似然是高斯分布，对这个联合分布的对数似然进行最大化就得到了参数， \(\frac{\sum\limits_{i=1}^Ny_ix_i}{N_1},\frac{\sum\limits_{i=1}^N(1-y_i)x_i}{N_0},\frac{N_1S_1+N_2S_2}{N},\frac{N_1}{N}\)。在朴素贝叶斯中，我们进一步对属性的各个维度之间的依赖关系作出假设，条件独立性假设大大减少了数据量的需求。

降维

我们知道，解决过拟合的问题除了正则化和添加数据之外，降维就是最好的方法。降维的思路来源于维度灾难的问题，我们知道 \(n\) 维球的体积为：
\[ CR^n \]
那么在球体积与边长为 \(2R\) 的超立方体比值为：
\[ \lim\limits_{n\rightarrow0}\frac{CR^n}{2^nR^n}=0 \]

这就是所谓的维度灾难，在高维数据中，主要样本都分布在立方体的边缘，所以数据集更加稀疏。

降维的算法分为：

1. 直接降维，特征选择
2. 线性降维，PCA，MDS等
3. 分线性，流形包括 Isomap，LLE 等

为了方便，我们首先将协方差矩阵（数据集）写成中心化的形式：
\[ \begin{align*}S&=\frac{1}{N}\sum\limits_{i=1}^N(x_i-\overline{x})(x_i-\overline{x})^T\\ &=\frac{1}{N}(x_1-\overline{x},x_2-\overline{x},\cdots,x_N-\overline{x})(x_1-\overline{x},x_2-\overline{x},\cdots,x_N-\overline{x})^T\\ &=\frac{1}{N}(X^T-\frac{1}{N}X^T\mathbb{I}_{N1}\mathbb{I}_{N1}^T)(X^T-\frac{1}{N}X^T\mathbb{I}_{N1}\mathbb{I}_{N1}^T)^T\\ &=\frac{1}{N}X^T(E_N-\frac{1}{N}\mathbb{I}_{N1}\mathbb{I}_{1N})(E_N-\frac{1}{N}\mathbb{I}_{N1}\mathbb{I}_{1N})^TX\\ &=\frac{1}{N}X^TH_NH_N^TX\\ &=\frac{1}{N}X^TH_NH_NX=\frac{1}{N}X^THX \end{align*} \]
这个式子利用了中心矩阵 $ H$的对称性，这也是一个投影矩阵。

线性降维-主成分分析 PCA

损失函数

主成分分析中，我们的基本想法是将所有数据投影到一个字空间中，从而达到降维的目标，为了寻找这个子空间，我们基本想法是：

1. 所有数据在子空间中更为分散
2. 损失的信息最小，即：在补空间的分量少

原来的数据很有可能各个维度之间是相关的，于是我们希望找到一组 \(p\) 个新的线性无关的单位基 \(u_i\)，降维就是取其中的 \(q\) 个基。于是对于一个样本 \(x_i\)，经过这个坐标变换后：
\[ \hat{x_i}=\sum\limits_{i=1}^p(u_i^Tx_i)u_i=\sum\limits_{i=1}^q(u_i^Tx_i)u_i+\sum\limits_{i=q+1}^p(u_i^Tx_i)u_i \]
对于数据集来说，我们首先将其中心化然后再去上面的式子的第一项，并使用其系数的平方平均作为损失函数并最大化：
\[ \begin{align*}J&=\frac{1}{N}\sum\limits_{i=1}^N\sum\limits_{j=1}^q((x_i-\overline{x})^Tu_j)^2\\ &=\sum\limits_{j=1}^qu_j^TSu_j\ ,\ s.t.\ u_j^Tu_j=1 \end{align*} \]
由于每个基都是线性无关的，于是每一个 \(u_j\) 的求解可以分别进行，使用拉格朗日乘子法：
\[ \mathop{argmax}_{u_j}L(u_j,\lambda)=\mathop{argmax}_{u_j}u_j^TSu_j+\lambda(1-u_j^Tu_j) \]
于是：
\[ Su_j=\lambda u_j \]
可见，我们需要的基就是协方差矩阵的本征矢。损失函数最大取在本征值前 \(q\) 个最大值。

下面看其损失的信息最少这个条件，同样适用系数的平方平均作为损失函数，并最小化：
\[ \begin{align*}J&=\frac{1}{N}\sum\limits_{i=1}^N\sum\limits_{j=q+1}^p((x_i-\overline{x})^Tu_j)^2\\ &=\sum\limits_{j=q+1}^pu_j^TSu_j\ ,\ s.t.\ u_j^Tu_j=1 \end{align*} \]
同样的：
\[ \mathop{argmin}_{u_j}L(u_j,\lambda)=\mathop{argmin}_{u_j}u_j^TSu_j+\lambda(1-u_j^Tu_j) \]
损失函数最小取在本征值剩下的个最小的几个值。数据集的协方差矩阵可以写成 \(S=U\Lambda U^T\)，直接对这个表达式当然可以得到本征矢。

SVD 与 PCoA

下面使用实际训练时常常使用的 SVD 直接求得这个 \(q\) 个本征矢。

对中心化后的数据集进行奇异值分解：
\[ HX=U\Sigma V^T,U^TU=E_N,V^TV=E_p,\Sigma:N\times p \]

于是：
\[ S=\frac{1}{N}X^THX=\frac{1}{N}X^TH^THX=\frac{1}{N}V\Sigma^T\Sigma V^T \]
因此，我们直接对中心化后的数据集进行 SVD，就可以得到特征值和特征向量 \(V\)，在新坐标系中的坐标就是：
\[ HX\cdot V \]
由上面的推导，我们也可以得到另一种方法 PCoA 主坐标分析，定义并进行特征值分解：
\[ T=HXX^TH=U\Sigma\Sigma^TU^T \]
由于：
\[ TU\Sigma=U\Sigma(\Sigma^T\Sigma) \]
于是可以直接得到坐标。这两种方法都可以得到主成分，但是由于方差矩阵是 \(p\times p\) 的，而 \(T\) 是 \(N\times N\) 的，所以对样本量较少的时候可以采用 PCoA的方法。

p-PCA

下面从概率的角度对 PCA 进行分析，概率方法也叫 p-PCA。我们使用线性模型，类似之前 LDA，我们选定一个方向，对原数据 \(x\in\mathbb{R}^p\) ，降维后的数据为 \(z\in\mathbb{R}^q,q<p\)。降维通过一个矩阵变换（投影）进行：
\[ \begin{align*} z&\sim\mathcal{N}(\mathbb{O}_{q1},\mathbb{I}_{qq})\\ x&=Wz+\mu+\varepsilon\\ \varepsilon&\sim\mathcal{N}(0,\sigma^2\mathbb{I}_{pp}) \end{align*} \]
对于这个模型，我么可以使用期望-最大（EM）的算法进行学习，在进行推断的时候需要求得 \(p(z|x)\)，推断的求解过程和线性高斯模型类似。
\[ \begin{align*} &p(z|x)=\frac{p(x|z)p(z)}{p(x)}\\ &\mathbb{E}[x]=\mathbb{E}[Wz+\mu+\varepsilon]=\mu\\ &Var[x]=WW^T+\sigma^2\mathbb{I}_{pp}\\ \Longrightarrow p(z|x)=\mathcal{N}(W^T(WW^T+&\sigma^2\mathbb{I})^{-1}(x-\mu),\mathbb{I}-W^T(WW^T+\sigma^2\mathbb{I})^{-1}W) \end{align*} \]

小结

降维是解决维度灾难和过拟合的重要方法，除了直接的特征选择外，我们还可以采用算法的途径对特征进行筛选，线性的降维方法以 PCA 为代表，在 PCA 中，我们只要直接对数据矩阵进行中心化然后求奇异值分解或者对数据的协方差矩阵进行分解就可以得到其主要维度。非线性学习的方法如流形学习将投影面从平面改为超曲面。

支撑向量机

支撑向量机（SVM）算法在分类问题中有着重要地位，其主要思想是最大化两类之间的间隔。按照数据集的特点：

1. 线性可分问题，如之前的感知机算法处理的问题
2. 线性可分，只有一点点错误点，如感知机算法发展出来的 Pocket 算法处理的问题
3. 非线性问题，完全不可分，如在感知机问题发展出来的多层感知机和深度学习

这三种情况对于 SVM 分别有下面三种处理手段：

1. hard-margin SVM
2. soft-margin SVM
3. kernel Method

SVM 的求解中，大量用到了 Lagrange 乘子法，首先对这种方法进行介绍。

约束优化问题

一般地，约束优化问题（原问题）可以写成：

\[ \begin{align*} &\min_{x\in\mathbb{R^p}}f(x)\\ &s.t.\ m_i(x)\le0,i=1,2,\cdots,M\\ &\ \ \ \ \ \ \ \ n_j(x)=0,j=1,2,\cdots,N \end{align*} \]

定义 Lagrange 函数：

\[ L(x,\lambda,\eta)=f(x)+\sum\limits_{i=1}^M\lambda_im_i(x)+\sum\limits_{i=1}^N\eta_in_i(x) \]

那么原问题可以等价于无约束形式：

\[ \min_{x\in\mathbb{R}^p}\max_{\lambda,\eta}L(x,\lambda,\eta)\ s.t.\ \lambda_i\ge0 \]

这是由于，当满足原问题的不等式约束的时候，\(\lambda_i=0\) 才能取得最大值，直接等价于原问题，如果不满足原问题的不等式约束，那么最大值就为 \(+\infty\) ，由于需要取最小值，于是不会取到这个情况。

这个问题的对偶形式：

\[ \max_{\lambda,\eta}\min_{x\in\mathbb{R}^p}L(x,\lambda,\eta)\ s.t.\ \lambda_i\ge0 \]

对偶问题是关于 $ , $ 的最大化问题。

由于：
\[ \max_{\lambda_i,\eta_j}\min_{x}L(x,\lambda_i,\eta_j)\le\min_{x}\max_{\lambda_i,\eta_j}L(x,\lambda_i,\eta_j) \]

证明：显然有 \(\min\limits_{x}L\le L\le\max\limits_{\lambda,\eta}L\)，于是显然有 \(\max\limits_{\lambda,\eta}\min\limits_{x}L\le L\)，且 \(\min\limits_{x}\max\limits_{\lambda,\eta}L\ge L\)。

对偶问题的解小于原问题，有两种情况：

1. 强对偶：可以取等于号
2. 弱对偶：不可以取等于号

其实这一点也可以通过一张图来说明：

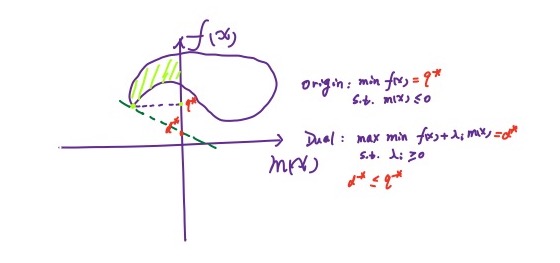
对于一个凸优化问题，有如下定理：

如果凸优化问题满足某些条件如 Slater 条件，那么它和其对偶问题满足强对偶关系。记问题的定义域为：\(\mathcal{D}=domf(x)\cap dom m_i(x)\cap domn_j(x)\)。于是 Slater 条件为：
\[ \exists \hat{x}\in Relint\mathcal{D}\ s.t.\ \forall i=1,2,\cdots,M,m_i(x)\lt0 \]
其中 Relint 表示相对内部（不包含边界的内部）。

1. 对于大多数凸优化问题，Slater 条件成立。
2. 松弛 Slater 条件，如果 M 个不等式约束中，有 K 个函数为仿射函数，那么只要其余的函数满足 Slater 条件即可。

上面介绍了原问题和对偶问题的对偶关系，但是实际还需要对参数进行求解，求解方法使用 KKT 条件进行：

KKT 条件和强对偶关系是等价关系。KKT 条件对最优解的条件为：

1. 可行域：
   \[ \begin{align*} m_i(x^*)\le0\\ n_j(x^*)=0\\ \lambda^*\ge0 \end{align*} \]

2. 互补松弛 \(\lambda^*m_i(x^*)=0,\forall m_i\)，对偶问题的最佳值为 \(d^*\)，原问题为 \(p^*\)
   \[ \begin{align*} d^*&=\max_{\lambda,\eta}g(\lambda,\eta)=g(\lambda^*,\eta^*)\\ &=\min_{x}L(x,\lambda^*,\eta^*)\\ &\le L(x^*,\lambda^*,\eta^*)\\ &=f(x^*)+\sum\limits_{i=1}^M\lambda^*m_i(x^*)\\ &\le f(x^*)=p^* \end{align*} \]
   为了满足相等，两个不等式必须成立，于是，对于第一个不等于号，需要有梯度为0条件，对于第二个不等于号需要满足互补松弛条件。

3. 梯度为0：\(\frac{\partial L(x,\lambda^*,\eta^*)}{\partial x}|_{x=x^*}=0\)

Hard-margin SVM

支撑向量机也是一种硬分类模型，在之前的感知机模型中，我们在线性模型的基础上叠加了符号函数，在几何直观上，可以看到，如果两类分的很开的话，那么其实会存在无穷多条线可以将两类分开。在 SVM 中，我们引入最大化间隔这个概念，间隔指的是数据和直线的距离的最小值，因此最大化这个值反映了我们的模型倾向。

分割的超平面可以写为：
\[ 0=w^Tx+b \]
那么最大化间隔（约束为分类任务的要求）：
\[ \begin{align*} \mathop{argmax}_{w,b}[\min_i\frac{|w^Tx_i+b|}{||w||}]\ s.t.\ y_i(w^Tx_i+b)>0\\ \Longrightarrow\mathop{argmax}_{w,b}[\min_i\frac{y_i(w^Tx_i+b)}{||w||}]\ s.t.\ y_i(w^Tx_i+b)>0 \end{align*} \]
对于这个约束 \(y_i(w^Tx_i+b)>0\)，不妨固定 \(\min y_i(w^Tx_i+b)=1>0\)，这是由于分开两类的超平面的系数经过比例放缩不会改变这个平面，这也相当于给超平面的系数作出了约束。化简后的式子可以表示为：

\[ \mathop{argmin}_{w,b}\frac{1}{2}w^Tw \ s.t.\ \min_iy_i(w^Tx_i+b)=1 \]
\[ \Rightarrow\mathop{argmin}_{w,b}\frac{1}{2}w^Tw\ s.t.\ y_i(w^Tx_i+b)\ge1,i=1,2,\cdots,N \]

这就是一个包含 \(N\) 个约束的凸优化问题，有很多求解这种问题的软件。

但是，如果样本数量或维度非常高，直接求解困难甚至不可解，于是需要对这个问题进一步处理。引入 Lagrange 函数：
\[ L(w,b,\lambda)=\frac{1}{2}w^Tw+\sum\limits_{i=1}^N\lambda_i(1-y_i(w^Tx_i+b)) \]
我们有原问题就等价于：
\[ \mathop{argmin}_{w,b}\max_{\lambda}L(w,b,\lambda_i)\ s.t.\ \lambda_i\ge0 \]
我们交换最小和最大值的符号得到对偶问题：
\[ \max_{\lambda_i}\min_{w,b}L(w,b,\lambda_i)\ s.t.\ \lambda_i\ge0 \]
由于不等式约束是仿射函数，对偶问题和原问题等价：

• \(b\)：\(\frac{\partial}{\partial b}L=0\Rightarrow\sum\limits_{i=1}^N\lambda_iy_i=0\)

• \(w\)：首先将 \(b\) 代入：
  \[ L(w,b,\lambda_i)=\frac{1}{2}w^Tw+\sum\limits_{i=1}^N\lambda_i(1-y_iw^Tx_i-y_ib)=\frac{1}{2}w^Tw+\sum\limits_{i=1}^N\lambda_i-\sum\limits_{i=1}^N\lambda_iy_iw^Tx_i \]
  所以：
  \[ \frac{\partial}{\partial w}L=0\Rightarrow w=\sum\limits_{i=1}^N\lambda_iy_ix_i \]

• 将上面两个参数代入：
  \[ L(w,b,\lambda_i)=-\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j+\sum\limits_{i=1}^N\lambda_i \]

因此，对偶问题就是：
\[ \max_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j+\sum\limits_{i=1}^N\lambda_i,\ s.t.\ \lambda_i\ge0 \]
从 KKT 条件得到超平面的参数：

原问题和对偶问题满足强对偶关系的充要条件为其满足 KKT 条件：
\[ \begin{align*} &\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0 \\&\lambda_k(1-y_k(w^Tx_k+b))=0(slackness\ complementary)\\ &\lambda_i\ge0\\ &1-y_i(w^Tx_i+b)\le0 \end{align*} \]

根据这个条件就得到了对应的最佳参数：
\[ \begin{gather*} \hat{w}=\sum\limits_{i=1}^N\lambda_iy_ix_i\\ \hat{b}=y_k-w^Tx_k=y_k-\sum\limits_{i=1}^N\lambda_iy_ix_i^Tx_k,\exists k,1-y_k(w^Tx_k+b)=0 \end{gather*} \]
于是这个超平面的参数 \(w\) 就是数据点的线性组合，最终的参数值就是部分满足 \(y_i(w^Tx_i+b)=1\)向量的线性组合（互补松弛条件给出），这些向量也叫支撑向量。

Soft-margin SVM

Hard-margin 的 SVM 只对可分数据可解，如果不可分的情况，我们的基本想法是在损失函数中加入错误分类的可能性。错误分类的个数可以写成：
\[ error=\sum\limits_{i=1}^N\mathbb{I}\{y_i(w^Tx_i+b)\lt1\} \]
这个函数不连续，可以将其改写为：
\[ error=\sum\limits_{i=1}^N\max\{0,1-y_i(w^Tx_i+b)\} \]
求和符号中的式子又叫做 Hinge Function。

将这个错误加入 Hard-margin SVM 中，于是：
\[ \mathop{argmin}_{w,b}\frac{1}{2}w^Tw+C\sum\limits_{i=1}^N\max\{0,1-y_i(w^Tx_i+b)\}\ s.t.\ y_i(w^Tx_i+b)\ge1-\xi_i,i=1,2,\cdots,N \]
这个式子中，常数 \(C\) 可以看作允许的错误水平，同时上式为了进一步消除 \(\max\) 符号，对数据集中的每一个观测，我们可以认为其大部分满足约束，但是其中部分违反约束，因此这部分约束变成 \(y_i(w^Tx+b)\ge1-\xi_i\)，其中 \(\xi_i=1-y_i(w^Tx_i+b)\)，进一步的化简：
\[ \mathop{argmin}_{w,b}\frac{1}{2}w^Tw+C\sum\limits_{i=1}^N\xi_i\ s.t.\ y_i(w^Tx_i+b)\ge1-\xi_i,\xi_i\ge0,i=1,2,\cdots,N \]

Kernel Method

核方法可以应用在很多问题上，在分类问题中，对于严格不可分问题，我们引入一个特征转换函数将原来的不可分的数据集变为可分的数据集，然后再来应用已有的模型。往往将低维空间的数据集变为高维空间的数据集后，数据会变得可分（数据变得更为稀疏）：

Cover TH：高维空间比低维空间更易线性可分。

应用在 SVM 中时，观察上面的 SVM 对偶问题：
\[ \max_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j+\sum\limits_{i=1}^N\lambda_i,\ s.t.\ \lambda_i\ge0 \]
在求解的时候需要求得内积，于是不可分数据在通过特征变换后，需要求得变换后的内积。我们常常很难求得变换函数的内积。于是直接引入内积的变换函数：
\[ \forall x,x'\in\mathcal{X},\exists\phi\in\mathcal{H}:x\rightarrow z\ s.t.\ k(x,x')=\phi(x)^T\phi(x) \]
称 \(k(x,x')\) 为一个正定核函数，其中\(\mathcal{H}\) 是 Hilbert 空间（完备的线性内积空间），如果去掉内积这个条件我们简单地称为核函数。

\(k(x,x')=\exp(-\frac{(x-x')^2}{2\sigma^2})\) 是一个核函数。

证明：
\[ \begin{align*} \exp(-\frac{(x-x')^2}{2\sigma^2})&=\exp(-\frac{x^2}{2\sigma^2})\exp(\frac{xx'}{\sigma^2})\exp(-\frac{x'^2}{2\sigma^2})\\ &=\exp(-\frac{x^2}{2\sigma^2})\sum\limits_{n=0}^{+\infty}\frac{x^nx'^n}{\sigma^{2n}n!}\exp(-\frac{x'^2}{2\sigma^2})\\ &=\exp(-\frac{x^2}{2\sigma^2})\varphi(x)\varphi(x')\exp(-\frac{x'^2}{2\sigma^2})\\ &=\phi(x)\phi(x') \end{align*} \]

正定核函数有下面的等价定义：

如果核函数满足：

1. 对称性
2. 正定性

那么这个核函数时正定核函数。

证明：

1. 对称性 \(\Leftrightarrow\) \(k(x,z)=k(z,x)\)，显然满足内积的定义
2. 正定性 \(\Leftrightarrow\) \(\forall N,x_1,x_2,\cdots,x_N\in\mathcal{X}\)，对应的 Gram Matrix \(K=[k(x_i,x_j)]\) 是半正定的。

要证：\(k(x,z)=\phi(x)^T\phi(z)\Leftrightarrow K\) 半正定+对称性。

1. \(\Rightarrow\)：首先，对称性是显然的，对于正定性：
   \[ K=\begin{pmatrix}k(x_1,x_2)&\cdots&k(x_1,x_N)\\\vdots&\vdots&\vdots\\k(x_N,x_1)&\cdots&k(x_N,x_N)\end{pmatrix} \]
   任意取 \(\alpha\in\mathbb{R}^N\)，即需要证明 \(\alpha^TK\alpha\ge0\)：
   \[ \alpha^TK\alpha=\sum\limits_{i,j}\alpha_i\alpha_jK_{ij}=\sum\limits_{i,j}\alpha_i\phi^T(x_i)\phi(x_j)\alpha_j=\sum\limits_{i}\alpha_i\phi^T(x_i)\sum\limits_{j}\alpha_j\phi(x_j) \]
   这个式子就是内积的形式，Hilbert 空间满足线性性，于是正定性的证。

2. \(\Leftarrow\)：对于 \(K\) 进行分解，对于对称矩阵 \(K=V\Lambda V^T\)，那么令 \(\phi(x_i)=\sqrt{\lambda_i}V_i\)，其中 \(V_i\)是特征向量，于是就构造了 \(k(x,z)=\sqrt{\lambda_i\lambda_j}V_i^TV_j\)

小结

分类问题在很长一段时间都依赖 SVM，对于严格可分的数据集，Hard-margin SVM 选定一个超平面，保证所有数据到这个超平面的距离最大，对这个平面施加约束，固定 \(y_i(w^Tx_i+b)=1\)，得到了一个凸优化问题并且所有的约束条件都是仿射函数，于是满足 Slater 条件，将这个问题变换成为对偶的问题，可以得到等价的解，并求出约束参数：
\[ \max_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j+\sum\limits_{i=1}^N\lambda_i,\ s.t.\ \lambda_i\ge0 \]
对需要的超平面参数的求解采用强对偶问题的 KKT 条件进行。
\[ \begin{align*} &\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0 \\&\lambda_k(1-y_k(w^Tx_k+b))=0(slackness\ complementary)\\ &\lambda_i\ge0\\ &1-y_i(w^Tx_i+b)\le0 \end{align*} \]
解就是：
\[ \begin{gather*} \hat{w}=\sum\limits_{i=1}^N\lambda_iy_ix_i\\ \hat{b}=y_k-w^Tx_k=y_k-\sum\limits_{i=1}^N\lambda_iy_ix_i^Tx_k,\exists k,1-y_k(w^Tx_k+b)=0 \end{gather*} \]
当允许一点错误的时候，可以在 Hard-margin SVM 中加入错误项。用 Hinge Function 表示错误项的大小，得到：
\[ \mathop{argmin}_{w,b}\frac{1}{2}w^Tw+C\sum\limits_{i=1}^N\xi_i\ s.t.\ y_i(w^Tx_i+b)\ge1-\xi_i,\xi_i\ge0,i=1,2,\cdots,N \]
对于完全不可分的问题，我们采用特征转换的方式，在 SVM 中，我们引入正定核函数来直接对内积进行变换，只要这个变换满足对称性和正定性，那么就可以用做核函数。

指数族分布

指数族是一类分布，包括高斯分布、伯努利分布、二项分布、泊松分布、Beta 分布、Dirichlet 分布、Gamma 分布等一系列分布。指数族分布可以写为统一的形式：
\[ p(x|\eta)=h(x)\exp(\eta^T\phi(x)-A(\eta))=\frac{1}{\exp(A(\eta))}h(x)\exp(\eta^T\phi(x)) \]
其中，\(\eta\) 是参数向量，\(A(\eta)\) 是对数配分函数（归一化因子）。

在这个式子中，$ (x)$ 叫做充分统计量，包含样本集合所有的信息，例如高斯分布中的均值和方差。充分统计量在在线学习中有应用，对于一个数据集，只需要记录样本的充分统计量即可。

对于一个模型分布假设（似然），那么我们在求解中，常常需要寻找一个共轭先验，使得先验与后验的形式相同，例如选取似然是二项分布，可取先验是 Beta 分布，那么后验也是 Beta 分布。指数族分布常常具有共轭的性质，于是我们在模型选择以及推断具有很大的便利。

共轭先验的性质便于计算，同时，指数族分布满足最大熵的思想（无信息先验），也就是说对于经验分布利用最大熵原理导出的分布就是指数族分布。

观察到指数族分布的表达式类似线性模型，事实上，指数族分布很自然地导出广义线性模型：
\[ \begin{gather*} y=f(w^Tx)\\ y|x\sim Exp Family \end{gather*} \]
在更复杂的概率图模型中，例如在无向图模型中如受限玻尔兹曼机中，指数族分布也扮演着重要作用。

在推断的算法中，例如变分推断中，指数族分布也会大大简化计算。

一维高斯分布

一维高斯分布可以写成：
\[ p(x|\theta)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-\mu)^2}{2\sigma^2}) \]
将这个式子改写：
\[ \begin{gather*} \frac{1}{\sqrt{2\pi\sigma^2}}\exp(-\frac{1}{2\sigma^2}(x^2-2\mu x+\mu^2))\\ =\exp(\log(2\pi\sigma^2)^{-1/2})\exp(-\frac{1}{2\sigma^2}\begin{pmatrix}-2\mu&1\end{pmatrix}\begin{pmatrix}x\\x^2\end{pmatrix}-\frac{\mu^2}{2\sigma^2}) \end{gather*} \]
所以：
\[ \eta=\begin{pmatrix}\frac{\mu}{\sigma^2}\\-\frac{1}{2\sigma^2}\end{pmatrix}=\begin{pmatrix}\eta_1\\\eta_2\end{pmatrix} \]
于是 \(A(\eta)\)：
\[ A(\eta)=-\frac{\eta_1^2}{4\eta_2}+\frac{1}{2}\log(-\frac{\pi}{\eta_2}) \]

充分统计量和对数配分函数的关系

对概率密度函数求积分：
\[ \begin{align*} \exp(A(\eta))&=\int h(x)\exp(\eta^T\phi(x))dx \end{align*} \]
两边对参数求导：
\[ \exp(A(\eta))A'(\eta)=\int h(x)\exp(\eta^T\phi(x))\phi(x)dx\\ \Longrightarrow A'(\eta)=\mathbb{E}_{p(x|\eta)}[\phi(x)] \]
类似的：
\[ A''(\eta)=Var_{p(x|\eta)}[\phi(x)] \]
由于方差为正，于是 \(A(\eta)\) 一定是凸函数。

充分统计量和极大似然估计

对于独立全同采样得到的数据集 \(\mathcal{D}=\{x_1,x_2,\cdots,x_N\}\)。
\[ \begin{align*} \eta_{MLE}&=\mathop{argmax}_\eta\sum\limits_{i=1}^N\log p(x_i|\eta)\\ &=\mathop{argmax}_\eta\sum\limits_{i=1}^N(\eta^T\phi(x_i)-A(\eta))\\ &\Longrightarrow A'(\eta_{MLE})=\frac{1}{N}\sum\limits_{i=1}^N\phi(x_i) \end{align*} \]
由此可以看到，为了估算参数，只需要知道充分统计量就可以了。

最大熵

信息熵记为：
\[ Entropy=\int-p(x)\log(p(x))dx \]

一般地，对于完全随机的变量（等可能），信息熵最大。

我们的假设为最大熵原则，假设数据是离散分布的，\(k\) 个特征的概率分别为 \(p_k\)，最大熵原理可以表述为：
\[ \max\{H(p)\}=\min\{\sum\limits_{k=1}^Kp_k\log p_k\}\ s.t.\ \sum\limits_{k=1}^Kp_k=1 \]
利用 Lagrange 乘子法：
\[ L(p,\lambda)=\sum\limits_{k=1}^Kp_k\log p_k+\lambda(1-\sum\limits_{k=1}^Kp_k) \]
于是可得：
\[ p_1=p_2=\cdots=p_K=\frac{1}{K} \]
因此等可能的情况熵最大。

一个数据集 \(\mathcal{D}\)，在这个数据集上的经验分布为 \(\hat{p}(x)=\frac{Count(x)}{N}\)，实际不可能满足所有的经验概率相同，于是在上面的最大熵原理中还需要加入这个经验分布的约束。

对任意一个函数，经验分布的经验期望可以求得为：
\[ \mathbb{E}_{\hat{p}}[f(x)]=\Delta \]
于是：
\[ \max\{H(p)\}=\min\{\sum\limits_{k=1}^Np_k\log p_k\}\ s.t.\ \sum\limits_{k=1}^Np_k=1,\mathbb{E}_p[f(x)]=\Delta \]
Lagrange 函数为：
\[ L(p,\lambda_0,\lambda)=\sum\limits_{k=1}^Np_k\log p_k+\lambda_0(1-\sum\limits_{k=1}^Np_k)+\lambda^T(\Delta-\mathbb{E}_p[f(x)]) \]
求导得到：
\[ \begin{gather*} \frac{\partial}{\partial p(x)}L=\sum\limits_{k=1}^N(\log p(x)+1)-\sum\limits_{k=1}^N\lambda_0-\sum\limits_{k=1}^N\lambda^Tf(x)\\ \Longrightarrow\sum\limits_{k=1}^N\log p(x)+1-\lambda_0-\lambda^Tf(x)=0 \end{gather*} \]
由于数据集是任意的，对数据集求和也意味着求和项里面的每一项都是0：
\[ p(x)=\exp(\lambda^Tf(x)+\lambda_0-1) \]
这就是指数族分布。

概率图模型

概率图模型使用图的方式表示概率分布。为了在图中添加各种概率，首先总结一下随机变量分布的一些规则：
\[ \begin{align*} &Sum\ Rule:p(x_1)=\int p(x_1,x_2)dx_2\\ &Product\ Rule:p(x_1,x_2)=p(x_1|x_2)p(x_2)\\ &Chain\ Rule:p(x_1,x_2,\cdots,x_p)=\prod\limits_{i=1}^pp(x_i|x_{i+1,x_{i+2} \cdots}x_p)\\ &Bayesian\ Rule:p(x_1|x_2)=\frac{p(x_2|x_1)p(x_1)}{p(x_2)} \end{align*} \]
可以看到，在链式法则中，如果数据维度特别高，那么的采样和计算非常困难，我们需要在一定程度上作出简化，在朴素贝叶斯中，作出了条件独立性假设。在 Markov 假设中，给定数据的维度是以时间顺序出现的，给定当前时间的维度，那么下一个维度与之前的维度独立。在 HMM 中，采用了齐次 Markov 假设。在 Markov 假设之上，更一般的，加入条件独立性假设，对维度划分集合 \(A,B,C\)，使得 \(X_A\perp X_B|X_C\)。

概率图模型采用图的特点表示上述的条件独立性假设，节点表示随机变量，边表示条件概率。概率图模型可以分为三大理论部分：

1. 表示：
   1. 有向图（离散）：贝叶斯网络
   2. 高斯图（连续）：高斯贝叶斯和高斯马尔可夫网路
   3. 无向图（离散）：马尔可夫网络
2. 推断
   1. 精确推断
   2. 近似推断
      1. 确定性近似（如变分推断）
      2. 随机近似（如 MCMC）
3. 学习
   1. 参数学习
      1. 完备数据
      2. 隐变量：E-M 算法
   2. 结构学习

有向图-贝叶斯网络

已知联合分布中，各个随机变量之间的依赖关系，那么可以通过拓扑排序（根据依赖关系）可以获得一个有向图。而如果已知一个图，也可以直接得到联合概率分布的因子分解：
\[ p(x_1,x_2,\cdots,x_p)=\prod\limits_{i=1}^pp(x_i|x_{parent(i)}) \]
那么实际的图中条件独立性是如何体现的呢？在局部任何三个节点，可以有三种结构：

 graph TB;

A((A))-->B((B));

B-->C((C));

\[ \begin{gather*} p(A,B,C)=p(A)p(B|A)p(C|B)=p(A)p(B|A)p(C|B,A)\\ \Longrightarrow p(C|B)=p(C|B,A)\\ \Leftrightarrow p(C|B)p(A|B)=p(C|A,B)p(A|B)=p(C,A|B)\\ \Longrightarrow C\perp A|B \end{gather*} \]

 graph TB;

B((B))-->A((A));

B-->C((C));

\[ \begin{gather*} p(A,B,C)=p(A|B)p(B)p(C|B)=p(B)p(A|B)p(C|A,B)\\ \Longrightarrow p(C|B)=p(C|B,A)\\ \Leftrightarrow p(C|B)p(A|B)=p(C|A,B)p(A|B)=p(C,A|B)\\ \Longrightarrow C\perp A|B \end{gather*} \]

 graph TB;

A((A))-->B((B));

C((C))-->B

\[ \begin{gather*} p(A,B,C)=p(A)p(C)p(B|C,A)=p(A)p(C|A)p(B|C,A)\\ \Longrightarrow p(C)=p(C|A)\\ \Leftrightarrow C\perp A\\ \end{gather*} \]

对这种结构，\(A,C\) 不与 \(B\) 条件独立。

从整体的图来看，可以引入 D 划分的概念。对于类似上面图 1和图 2的关系，引入集合A，B，那么满足 \(A\perp B|C\) 的 \(C\) 集合中的点与 \(A,B\) 中的点的关系都满足图 1，2，满足图3 关系的点都不在 \(C\) 中。D 划分应用在贝叶斯定理中：
\[ p(x_i|x_{-i})=\frac{p(x)}{\int p(x)dx_{i}}=\frac{\prod\limits_{j=1}^pp(x_j|x_{parents(j)})}{\int\prod\limits_{j=1}^pp(x_j|x_{parents(j)})dx_i} \]
可以发现，上下部分可以分为两部分，一部分是和 \(x_i\) 相关的，另一部分是和 \(x_i\) 无关的，而这个无关的部分可以相互约掉。于是计算只涉及和 \(x_i\) 相关的部分。

与 \(x_i\) 相关的部分可以写成：
\[ p(x_i|x_{parents(i)})p(x_{child(i)}|x_i) \]
这些相关的部分又叫做 Markov 毯。

实际应用的模型中，对这些条件独立性作出了假设，从单一到混合，从有限到无限（时间，空间）可以分为：

1. 朴素贝叶斯，单一的条件独立性假设 \(p(x|y)=\prod\limits_{i=1}^pp(x_i|y)\)，在 D 划分后，所有条件依赖的集合就是单个元素。
2. 高斯混合模型：混合的条件独立。引入多类别的隐变量 \(z_1, z_2,\cdots,z_k\)， \(p(x|z)=\mathcal{N}(\mu,\Sigma)\)，条件依赖集合为多个元素。
3. 与时间相关的条件依赖
   1. Markov 链
   2. 高斯过程（无限维高斯分布）
4. 连续：高斯贝叶斯网络
5. 组合上面的分类
   • GMM 与时序结合：动态模型
     • HMM（离散）
     • 线性动态系统 LDS（Kalman 滤波）
     • 粒子滤波（非高斯，非线性）

无向图-马尔可夫网络（马尔可夫随机场）

无向图没有了类似有向图的局部不同结构，在马尔可夫网络中，也存在 D 划分的概念。直接将条件独立的集合 \(x_A\perp x_B|x_C\) 划分为三个集合。这个也叫全局 Markov。对局部的节点，\(x\perp (X-Neighbour(\mathcal{x}))|Neighbour(x)\)。这也叫局部 Markov。对于成对的节点：\(x_i\perp x_j|x_{-i-j}\)，其中 \(i,j\) 不能相邻。这也叫成对 Markov。事实上上面三个点局部全局成对是相互等价的。

有了这个条件独立性的划分，还需要因子分解来实际计算。引入团的概念：

团，最大团：图中节点的集合，集合中的节点之间相互都是连接的叫做团，如果不能再添加节点，那么叫最大团。

利用这个定义进行的 \(x\) 所有维度的联合概率分布的因子分解为，假设有 \(K\) 个团，\(Z\) 就是对所有可能取值求和：
\[ \begin{align*}p(x)=\frac{1}{Z}\prod\limits_{i=1}^{K}\phi(x_{ci})\\ Z=\sum\limits_{x\in\mathcal{X}}\prod\limits_{i=1}^{K}\phi(x_{ci}) \end{align*} \]
其中 \(\phi(x_{ci})\) 叫做势函数，它必须是一个正值，可以记为：
\[ \phi(x_{ci})=\exp(-E(x_{ci})) \]
这个分布叫做 Gibbs 分布（玻尔兹曼分布）。于是也可以记为：\(p(x)=\frac{1}{Z}\exp(-\sum\limits_{i=1}^KE(x_{ci}))\)。这个分解和条件独立性等价（Hammesley-Clifford 定理），这个分布的形式也和指数族分布形式上相同，于是满足最大熵原理。

两种图的转换-道德图

我们常常想将有向图转为无向图，从而应用更一般的表达式。

1. 链式：

      graph TB;
    A((A))-->B((B));
    B-->C((C));

   直接去掉箭头，\(p(a,b,c)=p(a)p(b|a)p(c|b)=\phi(a,b)\phi(b,c)\)：

      graph TB;
    A((A))---B((B));
    B---C((C));

2. V 形：

      graph TB;
    B((B))-->A((A));
    B-->C((C));

   由于 \(p(a,b,c)=p(b)p(a|b)p(c|b)=\phi(a,b)\phi(b,c)\)，直接去掉箭头：

      graph TB;
    B((B))---A((A));
    B---C((C));

3. 倒 V 形：

      graph TB;
    A((A))-->B((B));
    C((C))-->B

   由于 \(p(a,b,c)=p(a)p(c)p(b|a,c)=\phi(a,b,c)\)，于是在 \(a,c\) 之间添加线：

      graph TD;
    a((a))---b((b));
    b---c((c));
    a---c;

   观察着三种情况可以概括为：

   1. 将每个节点的父节点两两相连
   2. 将有向边替换为无向边

更精细的分解-因子图

对于一个有向图，可以通过引入环的方式，可以将其转换为无向图（Tree-like graph），这个图就叫做道德图。但是我们上面的 BP 算法只对无环图有效，通过因子图可以变为无环图。

考虑一个无向图：

graph TD;
    a((a))---b((b));
    b---c((c));
    a---c;

可以将其转为：

graph TD;
    a((a))---f;
    f---b((b));
    f---c((c))

其中 \(f=f(a,b,c)\)。因子图不是唯一的，这是由于因式分解本身就对应一个特殊的因子图，将因式分解：\(p(x)=\prod\limits_{s}f_s(x_s)\) 可以进一步分解得到因子图。

推断

推断的主要目的是求各种概率分布，包括边缘概率，条件概率，以及使用 MAP 来求得参数。通常推断可以分为：

1. 精确推断
   1. Variable Elimination(VE)
   2. Belief Propagation(BP, Sum-Product Algo)，从 VE 发展而来
   3. Junction Tree，上面两种在树结构上应用，Junction Tree 在图结构上应用
2. 近似推断
   1. Loop Belief Propagation（针对有环图）
   2. Mente Carlo Interference：例如 Importance Sampling，MCMC
   3. Variational Inference

推断-变量消除（VE）

变量消除的方法是在求解概率分布的时候，将相关的条件概率先行求和或积分，从而一步步地消除变量，例如在马尔可夫链中：

graph LR;
    a((a))-->b((b));
    b-->c((c));
    c-->d((d))

\[ p(d)=\sum\limits_{a,b,c}p(a,b,c,d)=\sum\limits_cp(d|c)\sum\limits_bp(c|b)\sum\limits_ap(b|a)p(a) \]

变量消除的缺点很明显：

1. 计算步骤无法存储
2. 消除的最优次序是一个 NP-hard 问题

推断-信念传播（BP）

为了克服 VE 的第一个缺陷-计算步骤无法存储。我们进一步地对上面的马尔可夫链进行观察：

graph LR;
    a((a))-->b((b));
    b-->c((c));
    c-->d((d));
    d-->e((e));

要求 \(p(e)\)，当然使用 VE，从 \(a\) 一直消除到 \(d\)，记 \(\sum\limits_ap(a)p(b|a)=m_{a\to b(b)}\)，表示这是消除 \(a\) 后的关于 \(b\) 的概率，类似地，记 \(\sum\limits_bp(c|b)m_{a\to b}(b)=m_{b\to c}(c)\)。于是 \(p(e)=\sum\limits_dp(e|d)m_{b\to c}(c)\)。进一步观察，对 \(p(c)\)：
\[ p(c)=[\sum\limits_bp(c|b)\sum\limits_ap(b|a)p(a)]\cdot[\sum\limits_dp(d|c)\sum\limits_ep(e)p(e|d)] \]
我们发现了和上面计算 \(p(e)\) 类似的结构，这个式子可以分成两个部分，一部分是从 \(a\) 传播过来的概率，第二部分是从 $ e$ 传播过来的概率。

一般地，对于图（只对树形状的图）：

graph TD;
    a((a))---b((b));
    b---c((c));
    b---d((d));

这四个团（对于无向图是团，对于有向图就是概率为除了根的节点为1），有四个节点，三个边：
\[ p(a,b,c,d)=\frac{1}{Z}\phi_a(a)\phi_b(b)\phi_c(c)\phi_d(d)\cdot\phi_{ab}(a,b)\phi_{bc}(c,b)\phi_{bd}(d,b) \]
套用上面关于有向图的观察，如果求解边缘概率 \(p(a)\)，定义 \(m_{c\to b}(b)=\sum\limits_c\phi_c(c)\phi_{bc}(bc)\)，\(m_{d\to b}(b)=\sum\limits_d\phi_d(d)\phi_{bd}(bd)\)，\(m_{b\to a}(a)=\sum\limits_b\phi_{ba}(ba)\phi_b(b)m_{c\to b}(b)_{d\to b}m(b)\)，这样概率就一步步地传播到了 \(a\)：
\[ p(a)=\phi_a(a)m_{b\to a}(a) \]
写成一般的形式，对于相邻节点 \(i,j\)：
\[ m_{j\to i}(i)=\sum\limits_j\phi_j(j)\phi_{ij}(ij)\prod\limits_{k\in Neighbour(j)-i}m_{k\to j}(j) \]
这个表达式，就可以保存计算过程了，只要对每条边的传播分别计算，对于一个无向树形图可以递归并行实现：

1. 任取一个节点 \(a\) 作为根节点
2. 对这个根节点的邻居中的每一个节点，收集信息（计算入信息）
3. 对根节点的邻居，分发信息（计算出信息）

推断-Max-Product 算法

在推断任务中，MAP 也是常常需要的，MAP 的目的是寻找最佳参数：
\[ (\hat{a},\hat{b},\hat{c},\hat{d})=\mathop{argmax}_{a,b,c,d}p(a,b,c,d|E) \]
类似 BP，我们采用信息传递的方式来求得最优参数，不同的是，我们在所有信息传递中，传递的是最大化参数的概率，而不是将所有可能求和：
\[ m_{j\to i}=\max\limits_{j}\phi_j\phi_{ij}\prod\limits_{k\in Neighbour(j)-i}m_{k\to j} \]
于是对于上面的图：
\[ \max_a p(a,b,c,d)=\max_a\phi_a\phi_{ab}m_{c\to b}m_{d\to b} \]
这个算法是 Sum-Product 算法的改进，也是在 HMM 中应用给的 Viterbi 算法的推广。

期望最大

期望最大算法的目的是解决具有隐变量的混合模型的参数估计（极大似然估计）。MLE 对 \(p(x|\theta)\) 参数的估计记为：\(\theta_{MLE}=\mathop{argmax}\limits_\theta\log p(x|\theta)\)。EM 算法对这个问题的解决方法是采用迭代的方法：
\[ \theta^{t+1}=\mathop{argmax}\limits_{\theta}\int_z\log [p(x,z|\theta)]p(z|x,\theta^t)dz=\mathbb{E}_{z|x,\theta^t}[\log p(x,z|\theta)] \]
这个公式包含了迭代的两步：

1. E step：计算 \(\log p(x,z|\theta)\) 在概率分布 \(p(z|x,\theta^t)\) 下的期望
2. M step：计算使这个期望最大化的参数得到下一个 EM 步骤的输入

求证：\(\log p(x|\theta^t)\le\log p(x|\theta^{t+1})\)

证明：\(\log p(x|\theta)=\log p(z,x|\theta)-\log p(z|x,\theta)\)，对左右两边求积分：
\[ Left:\int_zp(z|x,\theta^t)\log p(x|\theta)dz=\log p(x|\theta) \]

\[ Right:\int_zp(z|x,\theta^t)\log p(x,z|\theta)dz-\int_zp(z|x,\theta^t)\log p(z|x,\theta)dz=Q(\theta,\theta^t)-H(\theta,\theta^t) \]

所以：
\[ \log p(x|\theta)=Q(\theta,\theta^t)-H(\theta,\theta^t) \]
由于 \(Q(\theta,\theta^t)=\int_zp(z|x,\theta^t)\log p(x,z|\theta)dz\)，而 \(\theta^{t+1}=\mathop{argmax}\limits_{\theta}\int_z\log [p(x,z|\theta)]p(z|x,\theta^t)dz\)，所以 \(Q(\theta^{t+1},\theta^t)\ge Q(\theta^t,\theta^t)\)。要证 \(\log p(x|\theta^t)\le\log p(x|\theta^{t+1})\)，需证：\(H(\theta^t,\theta^t)\ge H(\theta^{t+1},\theta^t)\)：
\[ \begin{align*}H(\theta^{t+1},\theta^t)-H(\theta^{t},\theta^t)&=\int_zp(z|x,\theta^{t})\log p(z|x,\theta^{t+1})dz-\int_zp(z|x,\theta^t)\log p(z|x,\theta^{t})dz\\ &=\int_zp(z|x,\theta^t)\log\frac{p(z|x,\theta^{t+1})}{p(z|x,\theta^t)}=-KL(p(z|x,\theta^t),p(z|x,\theta^{t+1}))\le0 \end{align*} \]
综合上面的结果：
\[ \log p(x|\theta^t)\le\log p(x|\theta^{t+1}) \]

根据上面的证明，我们看到，似然函数在每一步都会增大。进一步的，我们看 EM 迭代过程中的式子是怎么来的：
\[ \log p(x|\theta)=\log p(z,x|\theta)-\log p(z|x,\theta)=\log \frac{p(z,x|\theta)}{q(z)}-\log \frac{p(z|x,\theta)}{q(z)} \]
分别对两边求期望 \(\mathbb{E}_{q(z)}\)：
\[ \begin{align*} &Left:\int_zq(z)\log p(x|\theta)dz=\log p(x|\theta)\\ &Right:\int_zq(z)\log \frac{p(z,x|\theta)}{q(z)}dz-\int_zq(z)\log \frac{p(z|x,\theta)}{q(z)}dz=ELBO+KL(q(z),p(z|x,\theta)) \end{align*} \]
上式中，Evidence Lower Bound(ELBO)，是一个下界，所以 \(\log p(x|\theta)\ge ELBO\)，等于号取在 KL 散度为0是，即：\(q(z)=p(z|x,\theta)\)，EM 算法的目的是将 ELBO 最大化，根据上面的证明过程，在每一步 EM 后，求得了最大的ELBO，并根据这个使 ELBO 最大的参数代入下一步中：
\[ \hat{\theta}=\mathop{argmax}_{\theta}ELBO=\mathop{argmax}_\theta\int_zq(z)\log\frac{p(x,z|\theta)}{q(z)}dz \]
由于 $ q(z)=p(z|x,^t)$ 的时候，这一步的最大值才能取等号，所以：
\[ \begin{gather*} \hat{\theta}=\mathop{argmax}_{\theta}ELBO=\mathop{argmax}_\theta\int_zq(z)\log\frac{p(x,z|\theta)}{q(z)}dz=\mathop{argmax}_\theta\int_zp(z|x,\theta^t)\log\frac{p(x,z|\theta)}{p(z|x,\theta^t)}d z\\ =\mathop{argmax}_\theta\int_z p(z|x,\theta^t)\log p(x,z|\theta) \end{gather*} \]
这个式子就是上面 EM 迭代过程中的式子。

从 Jensen 不等式出发，也可以导出这个式子：
\[ \begin{gather*} \log p(x|\theta)=\log\int_zp(x,z|\theta)dz=\log\int_z\frac{p(x,z|\theta)q(z)}{q(z)}dz\\ =\log \mathbb{E}_{q(z)}[\frac{p(x,z|\theta)}{q(z)}]\ge \mathbb{E}_{q(z)}[\log\frac{p(x,z|\theta)}{q(z)}] \end{gather*} \]
其中，右边的式子就是 ELBO，等号在 $ p(x,z|)=Cq(z)$ 时成立。于是：
\[ \begin{gather*} \int_zq(z)dz=\frac{1}{C}\int_zp(x,z|\theta)dz=\frac{1}{C}p(x|\theta)=1\\ \Rightarrow q(z)=\frac{1}{p(x|\theta)}p(x,z|\theta)=p(z|x,\theta) \end{gather*} \]
我们发现，这个过程就是上面的最大值取等号的条件。

广义 EM

EM 模型解决了概率生成模型的参数估计的问题，通过引入隐变量 \(z\)，来学习 \(\theta\)，具体的模型对 \(z\) 有不同的假设。对学习任务 \(p(x|\theta)\)，就是学习任务 \(\frac{p(x,z|\theta)}{p(z|x,\theta)}\)。在这个式子中，我们假定了在 E 步骤中，\(q(z)=p(z|x,\theta)\)，但是这个\(p(z|x,\theta)\) 如果无法求解，那么必须使用采样（MCMC）或者变分推断等方法来近似推断这个后验。我们观察 KL 散度的表达式，为了最大化 ELBO，在固定的 \(\theta\) 时，我们需要最小化 KL 散度，于是：
\[ \hat{q}(z)=\mathop{argmin}_qKL(p,q)=\mathop{argmax}_qELBO \]
这就是广义 EM 的基本思路：

1. E step：
   \[ \hat{q}^{t+1}(z)=\mathop{argmax}_q\int_zq^t(z)\log\frac{p(x,z|\theta)}{q^t(z)}dz,fixed\ \theta \]

2. M step：
   \[ \hat{\theta}=\mathop{argmax}_\theta \int_zq^{t+1}(z)\log\frac{p(x,z|\theta)}{q^{t+1}(z)}dz,fixed\ \hat{q} \]

对于上面的积分：
\[ ELBO=\int_zq(z)\log\frac{p(x,z|\theta)}{q(z)}dz=\mathbb{E}_{q(z)}[p(x,z|\theta)]+Entropy(q(z)) \]
因此，我们看到，广义 EM 相当于在原来的式子中加入熵这一项。

EM 的推广

EM 算法类似于坐标上升法，固定部分坐标，优化其他坐标，再一遍一遍的迭代。如果在 EM 框架中，无法求解 \(z\) 后验概率，那么需要采用一些变种的 EM 来估算这个后验。

1. 基于平均场的变分推断，VBEM/VEM
2. 基于蒙特卡洛的EM，MCEM

高斯混合模型

为了解决高斯模型的单峰性的问题，我们引入多个高斯模型的加权平均来拟合多峰数据：
\[ p(x)=\sum\limits_{k=1}^K\alpha_k\mathcal{N}(\mu_k,\Sigma_k) \]
引入隐变量 \(z\)，这个变量表示对应的样本 \(x\) 属于哪一个高斯分布，这个变量是一个离散的随机变量：
\[ p(z=i)=p_i,\sum\limits_{i=1}^kp(z=i)=1 \]
作为一个生成式模型，高斯混合模型通过隐变量 \(z\) 的分布来生成样本。用概率图来表示：

graph LR;
    z((z))-->x((x))

其中，节点 \(z\) 就是上面的概率，\(x\) 就是生成的高斯分布。于是对 \(p(x)\)：
\[ p(x)=\sum\limits_zp(x,z)=\sum\limits_{k=1}^Kp(x,z=k)=\sum\limits_{k=1}^Kp(z=k)p(x|z=k) \]
因此：
\[ p(x)=\sum\limits_{k=1}^Kp_k\mathcal{N}(x|\mu_k,\Sigma_k) \]

极大似然估计

样本为 \(X=(x_1,x_2,\cdots,x_N)\)，$ (X,Z)$ 为完全参数，参数为 \(\theta=\{p_1,p_2,\cdots,p_K,\mu_1,\mu_2,\cdots,\mu_K\Sigma_1,\Sigma_2,\cdots,\Sigma_K\}\)。我们通过极大似然估计得到 \(\theta\) 的值：
\[ \begin{align*}\theta_{MLE}&=\mathop{argmax}\limits_{\theta}\log p(X)=\mathop{argmax}_{\theta}\sum\limits_{i=1}^N\log p(x_i)\\ &=\mathop{argmax}_\theta\sum\limits_{i=1}^N\log \sum\limits_{k=1}^Kp_k\mathcal{N}(x_i|\mu_k,\Sigma_k) \end{align*} \]
这个表达式直接通过求导，由于连加号的存在，无法得到解析解。因此需要使用 EM 算法。

EM 求解 GMM

EM 算法的基本表达式为：\(\theta^{t+1}=\mathop{argmax}\limits_{\theta}\mathbb{E}_{z|x,\theta_t}[p(x,z|\theta)]\)。套用 GMM 的表达式，对数据集来说：
\[ \begin{align*}Q(\theta,\theta^t)&=\sum\limits_z[\log\prod\limits_{i=1}^Np(x_i,z_i|\theta)]\prod \limits_{i=1}^Np(z_i|x_i,\theta^t)\\ &=\sum\limits_z[\sum\limits_{i=1}^N\log p(x_i,z_i|\theta)]\prod \limits_{i=1}^Np(z_i|x_i,\theta^t) \end{align*} \]
对于中间的那个求和号，展开，第一项为：
\[ \begin{align*} \sum\limits_z\log p(x_1,z_1|\theta)\prod\limits_{i=1}^Np(z_i|x_i,\theta^t)&=\sum\limits_z\log p(x_1,z_1|\theta)p(z_1|x_1,\theta^t)\prod\limits_{i=2}^Np(z_i|x_i,\theta^t)\\ &=\sum\limits_{z_1}\log p(x_1,z_1|\theta) p(z_1|x_1,\theta^t)\sum\limits_{z_2,\cdots,z_K}\prod\limits_{i=2}^Np(z_i|x_i,\theta^t)\\ &=\sum\limits_{z_1}\log p(x_1,z_1|\theta)p(z_1|x_1,\theta^t)\end{align*} \]
类似地，\(Q\) 可以写为：
\[ Q(\theta,\theta^t)=\sum\limits_{i=1}^N\sum\limits_{z_i}\log p(x_i,z_i|\theta)p(z_i|x_i,\theta^t) \]
对于 \(p(x,z|\theta)\)：
\[ p(x,z|\theta)=p(z|\theta)p(x|z,\theta)=p_z\mathcal{N}(x|\mu_z,\Sigma_z) \]
对 \(p(z|x,\theta^t)\)：
\[ p(z|x,\theta^t)=\frac{p(x,z|\theta^t)}{p(x|\theta^t)}=\frac{p_z^t\mathcal{N}(x|\mu_z^t,\Sigma_z^t)}{\sum\limits_kp_k^t\mathcal{N}(x|\mu_k^t,\Sigma_k^t)} \]
代入 \(Q\)：
\[ Q=\sum\limits_{i=1}^N\sum\limits_{z_i}\log p_{z_i}\mathcal{N(x_i|\mu_{z_i},\Sigma_{z_i})}\frac{p_{z_i}^t\mathcal{N}(x_i|\mu_{z_i}^t,\Sigma_{z_i}^t)}{\sum\limits_kp_k^t\mathcal{N}(x_i|\mu_k^t,\Sigma_k^t)} \]
下面需要对 \(Q\) 值求最大值：
\[ Q=\sum\limits_{k=1}^K\sum\limits_{i=1}^N[\log p_k+\log \mathcal{N}(x_i|\mu_k,\Sigma_k)]p(z_i=k|x_i,\theta^t) \]

1. \(p_k^{t+1}\)：
   \[ p_k^{t+1}=\mathop{argmax}_{p_k}\sum\limits_{k=1}^K\sum\limits_{i=1}^N[\log p_k+\log \mathcal{N}(x_i|\mu_k,\Sigma_k)]p(z_i=k|x_i,\theta^t)\ s.t.\ \sum\limits_{k=1}^Kp_k=1 \]
   即：
   \[ p_k^{t+1}=\mathop{argmax}_{p_k}\sum\limits_{k=1}^K\sum\limits_{i=1}^N\log p_kp(z_i=k|x_i,\theta^t)\ s.t.\ \sum\limits_{k=1}^Kp_k=1 \]
   引入 Lagrange 乘子：\(L(p_k,\lambda)=\sum\limits_{k=1}^K\sum\limits_{i=1}^N\log p_kp(z_i=k|x_i,\theta^t)-\lambda(1-\sum\limits_{k=1}^Kp_k)\)。所以：
   \[ \begin{gather*} \frac{\partial}{\partial p_k}L=\sum\limits_{i=1}^N\frac{1}{p_k}p(z_i=k|x_i,\theta^t)+\lambda=0\\ \Rightarrow \sum\limits_k\sum\limits_{i=1}^N\frac{1}{p_k}p(z_i=k|x_i,\theta^t)+\lambda\sum\limits_kp_k=0\\ \Rightarrow\lambda=-N \end{gather*} \]

   于是有：
   \[ p_k^{t+1}=\frac{1}{N}\sum\limits_{i=1}^Np(z_i=k|x_i,\theta^t) \]

2. \(\mu_k,\Sigma_k\)，这两个参数是无约束的，直接求导即可。

变分推断

我们已经知道概率模型可以分为，频率派的优化问题和贝叶斯派的积分问题。从贝叶斯角度来看推断，对于 \(\hat{x}\) 这样的新样本，需要得到：
\[ p(\hat{x}|X)=\int_\theta p(\hat{x},\theta|X)d\theta=\int_\theta p(\theta|X)p(\hat{x}|\theta,X)d\theta \]
如果新样本和数据集独立，那么推断就是概率分布依参数后验分布的期望。

我们看到，推断问题的中心是参数后验分布的求解，推断分为：

1. 精确推断
2. 近似推断-参数空间无法精确求解
   1. 确定性近似-如变分推断
   2. 随机近似-如 MCMC，MH，Gibbs

基于平均场假设的变分推断

我们记 \(Z\) 为隐变量和参数的集合，\(Z_i\) 为第 \(i\) 维的参数，于是，回顾一下 EM 中的推导：
\[ \log p(X)=\log p(X,Z)-\log p(Z|X)=\log\frac{p(X,Z)}{q(Z)}-\log\frac{p(Z|X)}{q(Z)} \]
左右两边分别积分：
\[ \begin{gather*} Left:\int_Zq(Z)\log p(X)dZ=\log p(X)\\ Right:\int_Z[\log \frac{p(X,Z)}{q(Z)}-\log \frac{p(Z|X)}{q(Z)}]q(Z)dZ=ELBO+KL(q,p) \end{gather*} \]
第二个式子可以写为变分和 KL 散度的和：
\[ L(q)+KL(q,p) \]
由于这个式子是常数，于是寻找 \(q\simeq p\) 就相当于对 \(L(q)\) 最大值。
\[ \hat{q}(Z)=\mathop{argmax}_{q(Z)}L(q) \]
假设 \(q(Z)\) 可以划分为 \(M\) 个组（平均场近似）：
\[ q(Z)=\prod\limits_{i=1}^Mq_i(Z_i) \]
因此，在 \(L(q)=\int_Zq(Z)\log p(X,Z)dZ-\int_Zq(Z)\log{q(Z)}\) 中，看 \(p(Z_j)\) ，第一项：
\[ \begin{align*}\int_Zq(Z)\log p(X,Z)dZ&=\int_Z\prod\limits_{i=1}^Mq_i(Z_i)\log p(X,Z)dZ\\ &=\int_{Z_j}q_j(Z_j)\int_{Z-Z_{j}}\prod\limits_{i\ne j}q_i(Z_i)\log p(X,Z)dZ\\ &=\int_{Z_j}q_j(Z_j)\mathbb{E}_{\prod\limits_{i\ne j}q_i(Z_i)}[\log p(X,Z)]dZ_j \end{align*} \]

第二项：
\[ \int_Zq(Z)\log q(Z)dZ=\int_Z\prod\limits_{i=1}^Mq_i(Z_i)\sum\limits_{i=1}^M\log q_i(Z_i)dZ \]
展开求和项第一项为：
\[ \int_Z\prod\limits_{i=1}^Mq_i(Z_i)\log q_1(Z_1)dZ=\int_{Z_1}q_1(Z_1)\log q_1(Z_1)dZ_1 \]
所以：
\[ \int_Zq(Z)\log q(Z)dZ=\sum\limits_{i=1}^M\int_{Z_i}q_i(Z_i)\log q_i(Z_i)dZ_i=\int_{Z_j}q_j(Z_j)\log q_j(Z_j)dZ_j+Const \]
两项相减，令 \(\mathbb{E}_{\prod\limits_{i\ne j}q_i(Z_i)}[\log p(X,Z)]=\log \hat{p}(X,Z_j)\) 可以得到：
\[ -\int_{Z_j}q_j(Z_j)\log\frac{q_j(Z_j)}{\hat{p}(X,Z_j)}dZ_j\le 0 \]
于是最大的 \(q_j(Z_j)=\hat{p}(X,Z_j)\) 才能得到最大值。我们看到，对每一个 \(q_j\)，都是固定其余的 \(q_i\)，求这个值，于是可以使用坐标上升的方法进行迭代求解，上面的推导针对单个样本，但是对数据集也是适用的。

基于平均场假设的变分推断存在一些问题：

1. 假设太强，\(Z\) 非常复杂的情况下，假设不适用
2. 期望中的积分，可能无法计算

SGVI

从 \(Z\) 到 \(X\) 的过程叫做生成过程或译码，反过来的额过程叫推断过程或编码过程，基于平均场的变分推断可以导出坐标上升的算法，但是这个假设在一些情况下假设太强，同时积分也不一定能算。我们知道，优化方法除了坐标上升，还有梯度上升的方式，我们希望通过梯度上升来得到变分推断的另一种算法。

我们的目标函数：
\[ \hat{q}(Z)=\mathop{argmax}_{q(Z)}L(q) \]
假定 \(q(Z)=q_\phi(Z)\)，是和 \(\phi\) 这个参数相连的概率分布。于是 \(\mathop{argmax}_{q(Z)}L(q)=\mathop{argmax}_{\phi}L(\phi)\)，其中 \(L(\phi)=\mathbb{E}_{q_\phi}[\log p_\theta(x^i,z)-\log q_\phi(z)]\)，这里 \(x^i\) 表示第 \(i\) 个样本。
\[ \begin{align*}\nabla_\phi L(\phi)&=\nabla_\phi\mathbb{E}_{q_\phi}[\log p_\theta(x^i,z)-\log q_\phi(z)]\\ &=\nabla_\phi\int q_\phi(z)[\log p_\theta(x^i,z)-\log q_\phi(z)]dz\\ &=\int\nabla_\phi q_\phi(z)[\log p_\theta(x^i,z)-\log q_\phi(z)]dz+\int q_\phi(z)\nabla_\phi [\log p_\theta(x^i,z)-\log q_\phi(z)]dz\\ &=\int\nabla_\phi q_\phi(z)[\log p_\theta(x^i,z)-\log q_\phi(z)]dz-\int q_\phi(z)\nabla_\phi \log q_\phi(z)dz\\ &=\int\nabla_\phi q_\phi(z)[\log p_\theta(x^i,z)-\log q_\phi(z)]dz-\int \nabla_\phi q_\phi(z)dz\\ &=\int\nabla_\phi q_\phi(z)[\log p_\theta(x^i,z)-\log q_\phi(z)]dz\\ &=\int q_\phi(\nabla_\phi\log q_\phi)(\log p_\theta(x^i,z)-\log q_\phi(z))dz\\ &=\mathbb{E}_{q_\phi}[(\nabla_\phi\log q_\phi)(\log p_\theta(x^i,z)-\log q_\phi(z))] \end{align*} \]
这个期望可以通过蒙特卡洛采样来近似，从而得到梯度，然后利用梯度上升的方法来得到参数：
\[ \begin{gather*} z^l\sim q_\phi(z)\\ \mathbb{E}_{q_\phi}[(\nabla_\phi\log q_\phi)(\log p_\theta(x^i,z)-\log q_\phi(z))]\sim \frac{1}{L}\sum\limits_{l=1}^L(\nabla_\phi\log q_\phi)(\log p_\theta(x^i,z)-\log q_\phi(z)) \end{gather*} \]
但是由于求和符号中存在一个对数项，于是直接采样的方差很大，需要采样的样本非常多。为了解决方差太大的问题，我们采用 Reparameterization 的技巧。

考虑：
\[ \nabla_\phi L(\phi)=\nabla_\phi\mathbb{E}_{q_\phi}[\log p_\theta(x^i,z)-\log q_\phi(z)] \]
我们取：\(z=g_\phi(\varepsilon,x^i),\varepsilon\sim p(\varepsilon)\)，于是对后验：\(z\sim q_\phi(z|x^i)\)，有 \(|q_\phi(z|x^i)dz|=|p(\varepsilon)d\varepsilon|\)。代入上面的梯度中：
\[ \begin{align*} \nabla_\phi L(\phi)&=\nabla_\phi\mathbb{E}_{q_\phi}[\log p_\theta(x^i,z)-\log q_\phi(z)]\\ &=\nabla_\phi L(\phi)=\nabla_\phi\int[\log p_\theta(x^i,z)-\log q_\phi(z)]q_\phi dz\\ &=\nabla_\phi\int[\log p_\theta(x^i,z)-\log q_\phi(z)]p_\varepsilon d\varepsilon\\ &=\mathbb{E}_{p(\varepsilon)}[\nabla_\phi[\log p_\theta(x^i,z)-\log q_\phi(z)]]\\ &=\mathbb{E}_{p(\varepsilon)}[\nabla_z[\log p_\theta(x^i,z)-\log q_\phi(z)]\nabla_\phi z]\\ &=\mathbb{E}_{p(\varepsilon)}[\nabla_z[\log p_\theta(x^i,z)-\log q_\phi(z)]\nabla_\phi g_\phi(\varepsilon,x^i)] \end{align*} \]
对这个式子进行蒙特卡洛采样，然后计算期望，得到梯度。

马尔可夫链蒙特卡洛

MCMC 是一种随机的近似推断，其核心就是基于采样的随机近似方法蒙特卡洛方法。对于采样任务来说，有下面一些常用的场景：

1. 采样作为任务，用于生成新的样本
2. 求和/求积分

采样结束后，我们需要评价采样出来的样本点是不是好的样本集：

1. 样本趋向于高概率的区域
2. 样本之间必须独立

具体采样中，采样是一个困难的过程：

1. 无法采样得到归一化因子，即无法直接对概率 $ p(x)=(x)$ 采样，常常需要对 CDF 采样，但复杂的情况不行
2. 如果归一化因子可以求得，但是对高维数据依然不能均匀采样（维度灾难），这是由于对 \(p\) 维空间，总的状态空间是 \(K^p\) 这么大，于是在这种情况下，直接采样也不行

因此需要借助其他手段，如蒙特卡洛方法中的拒绝采样，重要性采样和 MCMC。

蒙特卡洛方法

蒙特卡洛方法旨在求得复杂概率分布下的期望值：\(\mathbb{E}_{z|x}[f(z)]=\int p(z|x)f(z)dz\simeq\frac{1}{N}\sum\limits_{i=1}^Nf(z_i)\)，也就是说，从概率分布中取 \(N\) 个点，从而近似计算这个积分。采样方法有：

1. 概率分布采样，首先求得概率密度的累积密度函数 CDF，然后求得 CDF 的反函数，在0到1之间均匀采样，代入反函数，就得到了采样点。但是实际大部分概率分布不能得到 CDF。

2. Rejection Sampling 拒绝采样：对于概率分布 \(p(z)\)，引入简单的提议分布 \(q(z)\)，使得 \(\forall z_i,Mq(z_i)\ge p(z_i)\)。我们先在 $ q(z)$ 中采样，定义接受率：\(\alpha=\frac{p(z^i)}{Mq(z^i)}\le1\)。算法描述为：

   1. 取 \(z^i\sim q(z)\)。
   2. 在均匀分布中选取 \(u\)。
   3. 如果 \(u\le\alpha\)，则接受 \(z^i\)，否则，拒绝这个值。

3. Importance Sampling：直接对期望：\(\mathbb{E}_{p(z)}[f(z)]\) 进行采样。
   \[ \mathbb{E}_{p(z)}[f(z)]=\int p(z)f(z)dz=\int \frac{p(z)}{q(z)}f(z)q(z)dz\simeq\frac{1}{N}\sum\limits_{i=1}^Nf(z_i)\frac{p(z_i)}{q(z_i)} \]
   于是采样在 $ q(z)$ 中采样，并通过权重计算和。重要值采样对于权重非常小的时候，效率非常低。重要性采样有一个变种 Sampling-Importance-Resampling，这种方法，首先和上面一样进行采样，然后在采样出来的 \(N\) 个样本中，重新采样，这个重新采样，使用每个样本点的权重作为概率分布进行采样。

MCMC

马尔可夫链式一种时间状态都是离散的随机变量序列。我们关注的主要是齐次的一阶马尔可夫链。马尔可夫链满足：\(p(X_{t+1}|X_1,X_2,\cdots,X_t)=p(X_{t+1}|X_t)\)。这个式子可以写成转移矩阵的形式 \(p_{ij}=p(X_{t+1}=j|X_t=i)\)。我们有：
\[ \pi_{t+1}(x^*)=\int\pi_i(x)p_{x\to x^*}dx \]
如果存在 \(\pi=(\pi(1),\pi(2),\cdots),\sum\limits_{i=1}^{+\infty}\pi(i)=1\)，有上式成立，这个序列就叫马尔可夫链 \(X_t\) 的平稳分布，平稳分布就是表示在某一个时刻后，分布不再改变。MCMC 就是通过构建马尔可夫链概率序列，使其收敛到平稳分布 \(p(z)\)。引入细致平衡：\(\pi(x)p_{x\to x^*}=\pi(x^*)p_{x^*\to x}\)。如果一个分布满足细致平衡，那么一定满足平稳分布（反之不成立）：
\[ \int\pi(x)p_{x\to x^*}dx=\int\pi(x^*)p_{x^*\to x}dx=\pi(x^*) \]
细致平衡条件将平稳分布的序列和马尔可夫链的转移矩阵联系在一起了，通过转移矩阵可以不断生成样本点。假定随机取一个转移矩阵 \((Q=Q_{ij})\)，作为一个提议矩阵。我们有：
\[ p(z)\cdot Q_{z\to z^*}\alpha(z,z^*)=p(z^*)\cdot Q_{z^*\to z}\alpha(z^*,z) \]
取 ：
\[ \alpha(z,z^*)=\min\{1,\frac{p(z^*)Q_{z^*\to z}}{p(z)Q_{z\to z^*}}\} \]
则
\[ p(z)\cdot Q_{z\to z^*}\alpha(z,z^*)=\min\{p(z)Q_{z\to z^*},p(z^*)Q_{z^*\to z}\}=p(z^*)\cdot Q_{z^*\to z}\alpha(z^*,z) \]
于是，迭代就得到了序列，这个算法叫做 Metropolis-Hastings 算法：

1. 通过在0，1之间均匀分布取点 \(u\)
2. 生成 \(z^*\sim Q(z^*|z^{i-1})\)
3. 计算 \(\alpha\) 值
4. 如果 \(\alpha\ge u\)，则 \(z^i=z^*\)，否则 \(z^{i}=z^{i-1}\)

这样取的样本就服从 \(p(z)=\frac{\hat{p}(z)}{z_p}\sim \hat{p}(z)\)。

下面介绍另一种采样方式 Gibbs 采样，如果 \(z\) 的维度非常高，那么通过固定被采样的维度其余的维度来简化采样过程：\(z_i\sim p(z_i|z_{-i})\)：

1. 给定初始值 \(z_1^0,z_2^0,\cdots\)
2. 在 \(t+1\) 时刻，采样 \(z_i^{t+1}\sim p(z_i|z_{-i})\)，从第一个维度一个个采样。

Gibbs 采样方法是一种特殊的 MH 采样，可以计算 Gibbs 采样的接受率：
\[ \frac{p(z^*)Q_{z^*\to z}}{p(z)Q_{z\to z^*}}=\frac{p(z_i^*|z^*_{-i})p(z^*_{-i})p(z_i|z_{-i}^*)}{p(z_i|z_{-i})p(z_{-i})p(z_i^*|z_{-i})} \]
对于每个 Gibbs 采样步骤，\(z_{-i}=z_{-i}^*\)，这是由于每个维度 \(i\) 采样的时候，其余的参量保持不变。所以上式为1。于是 Gibbs 采样过程中，相当于找到了一个步骤，使得所有的接受率为 1。

平稳分布

定义随机矩阵：
\[ Q=\begin{pmatrix}Q_{11}&Q_{12}&\cdots&Q_{1K}\\\vdots&\vdots&\vdots&\vdots\\Q_{k1}&Q_{k2}&\cdots&Q_{KK}\end{pmatrix} \]
这个矩阵每一行或者每一列的和都是1。随机矩阵的特征值都小于等于1。假设只有一个特征值为 \(\lambda_i=1\)。于是在马尔可夫过程中：
\[ q^{t+1}(x=j)=\sum\limits_{i=1}^Kq^t(x=i)Q_{ij}\\ \Rightarrow q^{t+1}=q^t\cdot Q=q^1Q^t \]
于是有：
\[ q^{t+1}=q^1A\Lambda^t A^{-1} \]
如果 \(m\) 足够大，那么，\(\Lambda^m=diag(0,0,\cdots,1,\cdots,0)\)，则：\(q^{m+1}=q^{m}\) ，则趋于平稳分布了。马尔可夫链可能具有平稳分布的性质，所以我们可以构建马尔可夫链使其平稳分布收敛于需要的概率分布（设计转移矩阵）。

在采样过程中，需要经历一定的时间（燃烧期/混合时间）才能达到平稳分布。但是 MCMC 方法有一些问题：

1. 无法判断是否已经收敛
2. 燃烧期过长（维度太高，并且维度之间有关，可能无法采样到某些维度），例如在 GMM 中，可能无法采样到某些峰。于是在一些模型中，需要对隐变量之间的关系作出约束，如 RBM 假设隐变量之间无关。
3. 样本之间一定是有相关性的，如果每个时刻都取一个点，那么每个样本一定和前一个相关，这可以通过间隔一段时间采样。

隐马尔可夫模型

隐马尔可夫模型是一种概率图模型。我们知道，机器学习模型可以从频率派和贝叶斯派两个方向考虑，在频率派的方法中的核心是优化问题，而在贝叶斯派的方法中，核心是积分问题，也发展出来了一系列的积分方法如变分推断，MCMC 等。概率图模型最基本的模型可以分为有向图（贝叶斯网络）和无向图（马尔可夫随机场）两个方面，例如 GMM，在这些基本的模型上，如果样本之间存在关联，可以认为样本中附带了时序信息，从而样本之间不独立全同分布的，这种模型就叫做动态模型，隐变量随着时间发生变化，于是观测变量也发生变化：

graph LR;
    z1-->z2-->z3;

根据状态变量的特点，可以分为：

1. HMM，状态变量（隐变量）是离散的
2. Kalman 滤波，状态变量是连续的，线性的
3. 粒子滤波，状态变量是连续，非线性的

HMM

HMM 用概率图表示为：

graph TD;
t1-->t2;
subgraph four
    t4-->x4((x4))
end
subgraph three
    t3-->x3((x3))
end
subgraph two
    t2-->x2((x2))
end
subgraph one
    t1-->x1((x1))
end

t2-->t3;
t3-->t4;

上图表示了四个时刻的隐变量变化。用参数 \(\lambda=(\pi,A,B)\) 来表示，其中 \(\pi\) 是开始的概率分布，\(A\) 为状态转移矩阵，\(B\) 为发射矩阵。

下面使用 $ o_t$ 来表示观测变量，\(O\) 为观测序列，\(V=\{v_1,v_2,\cdots,v_M\}\) 表示观测的值域，\(i_t\) 表示状态变量，\(I\) 为状态序列，\(Q=\{q_1,q_2,\cdots,q_N\}\) 表示状态变量的值域。定义 \(A=(a_{ij}=p(i_{t+1}=q_j|i_t=q_i))\) 表示状态转移矩阵，\(B=(b_j(k)=p(o_t=v_k|i_t=q_j))\) 表示发射矩阵。

在 HMM 中，有两个基本假设：

1. 齐次 Markov 假设（未来只依赖于当前）：
   \[ p(i_{t+1}|i_t,i_{t-1},\cdots,i_1,o_t,o_{t-1},\cdots,o_1)=p(i_{t+1}|i_t) \]

2. 观测独立假设：
   \[ p(o_t|i_t,i_{t-1},\cdots,i_1,o_{t-1},\cdots,o_1)=p(o_t|i_t) \]

HMM 要解决三个问题：

1. Evaluation：\(p(O|\lambda)\)，Forward-Backward 算法
2. Learning：\(\lambda=\mathop{argmax}\limits_{\lambda}p(O|\lambda)\)，EM 算法（Baum-Welch）
3. Decoding：\(I=\mathop{argmax}\limits_{I}p(I|O,\lambda)\)，Vierbi 算法
   1. 预测问题：\(p(i_{t+1}|o_1,o_2,\cdots,o_t)\)
   2. 滤波问题：\(p(i_t|o_1,o_2,\cdots,o_t)\)

Evaluation

\[ p(O|\lambda)=\sum\limits_{I}p(I,O|\lambda)=\sum\limits_{I}p(O|I,\lambda)p(I|\lambda) \]

\[ p(I|\lambda)=p(i_1,i_2,\cdots,i_t|\lambda)=p(i_t|i_1,i_2,\cdots,i_{t-1},\lambda)p(i_1,i_2,\cdots,i_{t-1}|\lambda) \]

根据齐次 Markov 假设：
\[ p(i_t|i_1,i_2,\cdots,i_{t-1},\lambda)=p(i_t|i_{t-1})=a_{i_{t-1}i_t} \]
所以：
\[ p(I|\lambda)=\pi_1\prod\limits_{t=2}^Ta_{i_{t-1},i_t} \]
又由于：
\[ p(O|I,\lambda)=\prod\limits_{t=1}^Tb_{i_t}(o_t) \]
于是：
\[ p(O|\lambda)=\sum\limits_{I}\pi_{i_1}\prod\limits_{t=2}^Ta_{i_{t-1},i_t}\prod\limits_{t=1}^Tb_{i_t}(o_t) \]
我们看到，上面的式子中的求和符号是对所有的观测变量求和，于是复杂度为 \(O(N^T)\)。

下面，记 \(\alpha_t(i)=p(o_1,o_2,\cdots,o_t,i_t=q_i|\lambda)\)，所以，\(\alpha_T(i)=p(O,i_T=q_i|\lambda)\)。我们看到：
\[ p(O|\lambda)=\sum\limits_{i=1}^Np(O,i_T=q_i|\lambda)=\sum\limits_{i=1}^N\alpha_T(i) \]
对 \(\alpha_{t+1}(j)\)：
\[ \begin{align*}\alpha_{t+1}(j)&=p(o_1,o_2,\cdots,o_{t+1},i_{t+1}=q_j|\lambda)\\ &=\sum\limits_{i=1}^Np(o_1,o_2,\cdots,o_{t+1},i_{t+1}=q_j,i_t=q_i|\lambda)\\ &=\sum\limits_{i=1}^Np(o_{t+1}|o_1,o_2,\cdots,i_{t+1}=q_j,i_t=q_i|\lambda)p(o_1,\cdots,o_t,i_t=q_i,i_{t+1}=q_j|\lambda) \end{align*} \]
利用观测独立假设：
\[ \begin{align*}\alpha_{t+1}(j)&=\sum\limits_{i=1}^Np(o_{t+1}|i_{t+1}=q_j)p(o_1,\cdots,o_t,i_t=q_i,i_{t+1}=q_j|\lambda)\\ &=\sum\limits_{i=1}^Np(o_{t+1}|i_{t+1}=q_j)p(i_{t+1}=q_j|o_1,\cdots,o_t,i_t=q_i,\lambda)p(o_1,\cdots,o_t,i_t=q_i|\lambda)\\ &=\sum\limits_{i=1}^Nb_{j}(o_t)a_{ij}\alpha_t(i) \end{align*} \]
上面利用了齐次 Markov 假设得到了一个递推公式，这个算法叫做前向算法。

还有一种算法叫做后向算法，定义 \(\beta_t(i)=p(o_{t+1},o_{t+1},\cdots，o_T|i_t=i,\lambda)\)：
\[ \begin{align*}p(O|\lambda)&=p(o_1,\cdots,o_T|\lambda)\\ &=\sum\limits_{i=1}^Np(o_1,o_2,\cdots,o_T,i_1=q_i|\lambda)\\ &=\sum\limits_{i=1}^Np(o_1,o_2,\cdots,o_T|i_1=q_i,\lambda)\pi_i\\ &=\sum\limits_{i=1}^Np(o_1|o_2,\cdots,o_T,i_1=q_i,\lambda)p(o_2,\cdots,o_T|i_1=q_i,\lambda)\pi_i\\ &=\sum\limits_{i=1}^Nb_i(o_1)\pi_i\beta_1(i) \end{align*} \]
对于这个 \(\beta_1(i)\)：
\[ \begin{align*}\beta_t(i)&=p(o_{t+1},\cdots,o_T|i_t=q_i)\\ &=\sum\limits_{j=1}^Np(o_{t+1},o_{t+2},\cdots,o_T,i_{t+1}=q_j|i_t=q_i)\\ &=\sum\limits_{j=1}^Np(o_{t+1},\cdots,o_T|i_{t+1}=q_j,i_t=q_i)p(i_{t+1}=q_j|i_t=q_i)\\ &=\sum\limits_{j=1}^Np(o_{t+1},\cdots,o_T|i_{t+1}=q_j)a_{ij}\\ &=\sum\limits_{j=1}^Np(o_{t+1}|o_{t+2},\cdots,o_T,i_{t+1}=q_j)p(o_{t+2},\cdots,o_T|i_{t+1}=q_j)a_{ij}\\ &=\sum\limits_{j=1}^Nb_j(o_{t+1})a_{ij}\beta_{t+1}(j) \end{align*} \]
于是后向地得到了第一项。

Learning

为了学习得到参数的最优值，在 MLE 中：
\[ \lambda_{MLE}=\mathop{argmax}_\lambda p(O|\lambda) \]
我们采用 EM 算法（在这里也叫 Baum Welch 算法），用上标表示迭代：
\[ \theta^{t+1}=\mathop{argmax}_{\theta}\int_z\log p(X,Z|\theta)p(Z|X,\theta^t)dz \]
其中，\(X\) 是观测变量，\(Z\) 是隐变量序列。于是：
\[ \lambda^{t+1}=\mathop{argmax}_\lambda\sum\limits_I\log p(O,I|\lambda)p(I|O,\lambda^t)\\ =\mathop{argmax}_\lambda\sum\limits_I\log p(O,I|\lambda)p(O,I|\lambda^t) \]
这里利用了 \(p(O|\lambda^t)\) 和\(\lambda\) 无关。将 Evaluation 中的式子代入：
\[ \sum\limits_I\log p(O,I|\lambda)p(O,I|\lambda^t)=\sum\limits_I[\log \pi_{i_1}+\sum\limits_{t=2}^T\log a_{i_{t-1},i_t}+\sum\limits_{t=1}^T\log b_{i_t}(o_t)]p(O,I|\lambda^t) \]
对 \(\pi^{t+1}\)：
\[ \begin{align*}\pi^{t+1}&=\mathop{argmax}_\pi\sum\limits_I[\log \pi_{i_1}p(O,I|\lambda^t)]\\ &=\mathop{argmax}_\pi\sum\limits_I[\log \pi_{i_1}\cdot p(O,i_1,i_2,\cdots,i_T|\lambda^t)] \end{align*} \]
上面的式子中，对 \(i_2,i_2,\cdots,i_T\) 求和可以将这些参数消掉：
\[ \pi^{t+1}=\mathop{argmax}_\pi\sum\limits_{i_1}[\log \pi_{i_1}\cdot p(O,i_1|\lambda^t)] \]
上面的式子还有对 \(\pi\) 的约束 \(\sum\limits_i\pi_i=1\)。定义 Lagrange 函数：
\[ L(\pi,\eta)=\sum\limits_{i=1}^N\log \pi_i\cdot p(O,i_1=q_i|\lambda^t)+\eta(\sum\limits_{i=1}^N\pi_i-1) \]
于是：
\[ \frac{\partial L}{\partial\pi_i}=\frac{1}{\pi_i}p(O,i_1=q_i|\lambda^t)+\eta=0 \]
对上式求和：
\[ \sum\limits_{i=1}^Np(O,i_1=q_i|\lambda^t)+\pi_i\eta=0\Rightarrow\eta=-p(O|\lambda^t) \]
所以：
\[ \pi_i^{t+1}=\frac{p(O,i_1=q_i|\lambda^t)}{p(O|\lambda^t)} \]

Decoding

Decoding 问题表述为：
\[ I=\mathop{argmax}\limits_{I}p(I|O,\lambda) \]
我们需要找到一个序列，其概率最大，这个序列就是在参数空间中的一个路径，可以采用动态规划的思想。

定义：
\[ \delta_{t}(j)=\max\limits_{i_1,\cdots,i_{t-1}}p(o_1,\cdots,o_t,i_1,\cdots,i_{t-1},i_t=q_i) \]
于是：
\[ \delta_{t+1}(j)=\max\limits_{1\le i\le N}\delta_t(i)a_{ij}b_j(o_{t+1}) \]
这个式子就是从上一步到下一步的概率再求最大值。记这个路径为：
\[ \psi_{t+1}(j)=\mathop{argmax}\limits_{1\le i\le N}\delta_t(i)a_{ij} \]

小结

HMM 是一种动态模型，是由混合树形模型和时序结合起来的一种模型（类似 GMM + Time）。对于类似 HMM 的这种状态空间模型，普遍的除了学习任务（采用 EM ）外，还有推断任务，推断任务包括：

1. 译码 Decoding：\(p(z_1,z_2,\cdots,z_t|x_1,x_2,\cdots,x_t)\)

2. 似然概率：\(p(X|\theta)\)

3. 滤波：$ p(z_t|x_1,,x_t)$，Online
   \[ p(z_t|x_{1:t})=\frac{p(x_{1:t},z_t)}{p(x_{1:t})}=C\alpha_t(z_t) \]

4. 平滑：\(p(z_t|x_1,\cdots,x_T)\)，Offline
   \[ p(z_t|x_{1:T})=\frac{p(x_{1:T},z_t)}{p(x_{1:T})}=\frac{\alpha_t(z_t)p(x_{t+1:T}|x_{1:t},z_t)}{p(x_{1:T})} \]
   根据概率图的条件独立性，有：
   \[ p(z_t|x_{1:T})=\frac{\alpha_t(z_t)p(x_{t+1:T}|z_t)}{p(x_{1:T})}=C\alpha_t(z_t)\beta_t(z_t) \]
   这个算法叫做前向后向算法。

5. 预测：\(p(z_{t+1},z_{t+2}|x_1,\cdots,x_t),p(x_{t+1},x_{t+2}|x_1,\cdots,x_t)\)
   \[ p(z_{t+1}|x_{1:t})=\sum_{z_t}p(z_{t+1},z_t|x_{1:t})=\sum\limits_{z_t}p(z_{t+1}|z_t)p(z_t|x_{1:t}) \]

   \[ p(x_{t+1}|x_{1:t})=\sum\limits_{z_{t+1}}p(x_{t+1},z_{t+1}|x_{1:t})=\sum\limits_{z_{t+1}}p(x_{t+1}|z_{t+1})p(z_{t+1}|x_{1:t}) \]

线性动态系统

HMM 模型适用于隐变量是离散的值的时候，对于连续隐变量的 HMM，常用线性动态系统描述线性高斯模型的态变量，使用粒子滤波来表述非高斯非线性的态变量。

LDS 又叫卡尔曼滤波，其中，线性体现在上一时刻和这一时刻的隐变量以及隐变量和观测之间：
\[ \begin{align*} z_t&=A\cdot z_{t-1}+B+\varepsilon\\ x_t&=C\cdot z_t+D+\delta\\ \varepsilon&\sim\mathcal{N}(0,Q)\\ \delta&\sim\mathcal{N}(0,R) \end{align*} \]
类比 HMM 中的几个参数：
\[ \begin{align*} p(z_t|z_{t-1})&\sim\mathcal{N}(A\cdot z_{t-1}+B,Q)\\ p(x_t|z_t)&\sim\mathcal{N}(C\cdot z_t+D,R)\\ z_1&\sim\mathcal{N}(\mu_1,\Sigma_1) \end{align*} \]
在含时的概率图中，除了对参数估计的学习问题外，在推断任务中，包括译码，证据概率，滤波，平滑，预测问题，LDS 更关心滤波这个问题：\(p(z_t|x_1,x_2,\cdots,x_t)\)。类似 HMM 中的前向算法，我们需要找到一个递推关系。
\[ p(z_t|x_{1:t})=p(x_{1:t},z_t)/p(x_{1:t})=Cp(x_{1:t},z_t) \]
对于 \(p(x_{1:t},z_t)\)：
\[ \begin{align*}p(x_{1:t},z_t)&=p(x_t|x_{1:t-1},z_t)p(x_{1:t-1},z_t)=p(x_t|z_t)p(x_{1:t-1},z_t)\\ &=p(x_t|z_t)p(z_t|x_{1:t-1})p(x_{1:t-1})=Cp(x_t|z_t)p(z_t|x_{1:t-1})\\ \end{align*} \]
我们看到，右边除了只和观测相关的常数项，还有一项是预测任务需要的概率。对这个值：
\[ \begin{align*} p(z_t|x_{1:t-1})&=\int_{z_{t-1}}p(z_t,z_{t-1}|x_{1:t-1})dz_{t-1}\\ &=\int_{z_{t-1}}p(z_t|z_{t-1},x_{1:t-1})p(z_{t-1}|x_{1:t-1})dz_{t-1}\\ &=\int_{z_{t-1}}p(z_t|z_{t-1})p(z_{t-1}|x_{1:t-1})dz_{t-1} \end{align*} \]
我们看到，这又化成了一个滤波问题。于是我们得到了一个递推公式：

1. \(t=1\)，\(p(z_1|x_1)\)，称为 update 过程，然后计算 \(p(z_2|x_1)\)，通过上面的积分进行，称为 prediction 过程。
2. \(t=2\)，\(p(z_2|x_2,x_1)\) 和 \(p(z_3|x_1,x_2)\)

我们看到，这个过程是一个 Online 的过程，对于我们的线性高斯假设，这个计算过程都可以得到解析解。

1. Prediction：
   \[ p(z_t|x_{1:t-1})=\int_{z_{t-1}}p(z_t|z_{t-1})p(z_{t-1}|x_{1:t-1})dz_{t-1}=\int_{z_{t-1}}\mathcal{N}(Az_{t-1}+B,Q)\mathcal{N}(\mu_{t-1},\Sigma_{t-1})dz_{t-1} \]
   其中第二个高斯分布是上一步的 Update 过程，所以根据线性高斯模型，直接可以写出这个积分：
   \[ p(z_t|x_{1:t-1})=\mathcal{N}(A\mu_{t-1}+B,Q+A\Sigma_{t-1}A^T) \]

2. Update:
   \[ p(z_t|x_{1:t})\propto p(x_t|z_t)p(z_t|x_{1:t-1}) \]
   同样利用线性高斯模型，也可以直接写出这个高斯分布。

粒子滤波

Kalman 滤波根据线性高斯模型可以求得解析解，但是在非线性，非高斯的情况，是无法得到解析解的，对这类一般的情况，我们叫做粒子滤波，我们需要求得概率分布，需要采用采样的方式。

我们希望应用 Monte Carlo 方法来进行采样，对于一个概率分布，如果我们希望计算依这个分布的某个函数 \(f(z)\) 的期望，可以利用某种抽样方法，在这个概率分布中抽取 \(N\) 个样本，则 \(\mathbb{E}[f(z)]\simeq\frac{1}{N}\sum\limits_{i=1}^Nf(z_i)\)。但是如果这个概率十分复杂，那么采样比较困难。对于复杂的概率分布，我们可以通过一个简单的概率分布 \(q(z)\) 作为桥梁（重要值采样）:
\[ \mathbb{E}[f(z)]=\int_zf(z)p(z)dz=\int_zf(z)\frac{p(z)}{q(z)}q(z)dz=\sum\limits_{i=1}^Nf(z_i)\frac{p(z_i)}{q(z_i)} \]
于是直接通过对 \(q(z)\) 采样，然后对每一个采样的样本应用权重就得到了期望的近似，当然为了概率分布的特性，我们需要对权重进行归一化。

在滤波问题中，需要求解 \(p(z_t|x_{1:t})\)，其权重为：
\[ w_t^i=\frac{p(z_t^i|x_{1:t})}{q(z_t^i|x_{1:t})},i=1,2,\cdots,N \]
于是在每一个时刻 \(t\)，都需要采样 \(N\) 个点，但是即使采样了这么多点，分子上面的那一项也十分难求，于是希望找到一个关于权重的递推公式。为了解决这个问题，引入序列重要性采样（SIS）。

SIS

在 SIS 中，解决的问题是 \(p(z_{1:t}|x_{1:t})\)。
\[ w_t^i\propto\frac{p(z_{1:t}|x_{1:t})}{q(z_{1:t}|x_{1:t})} \]
根据 LDS 中的推导：
\[ \begin{align*}p(z_{1:t}|x_{1:t})\propto p(x_{1:t},z_{1:t})&=p(x_t|z_{1:t},x_{1:t-1})p(z_{1:t},x_{1:t-1})\\ &=p(x_t|z_t)p(z_t|x_{1:t-1},z_{1:t-1})p(x_{1:t-1},z_{1:t-1})\\ &=p(x_t|z_t)p(z_t|z_{t-1})p(x_{1:t-1},z_{1:t-1})\\ &\propto p(x_t|z_t)p(z_t|z_{t-1})p(z_{1:t-1}|x_{1:t-1}) \end{align*} \]
于是分子的递推式就得到了。对于提议分布的分母，可以取：
\[ q(z_{1:t}|x_{1:t})=q(z_t|z_{1:t-1},x_{1:t})q(z_{1:t-1}|x_{1:t-1}) \]
所以有：
\[ w_t^i\propto\frac{p(z_{1:t}|x_{1:t})}{q(z_{1:t}|x_{1:t})}\propto \frac{p(x_t|z_t)p(z_t|z_{t-1})p(z_{1:t-1}|x_{1:t-1})}{q(z_t|z_{1:t-1},x_{1:t})q(z_{1:t-1}|x_{1:t-1})}=\frac{p(x_t|z_t)p(z_t|z_{t-1})}{q(z_t|z_{1:t-1},x_{1:t})}w_{t-1}^i \]
我们得到的对权重的算法为：

1. \(t-1\) 时刻，采样完成并计算得到权重
2. t 时刻，根据 \(q(z_t|z_{1:t-1},x_{1:t})\) 进行采样得到 \(z_t^i\)。然后计算得到 \(N\) 个权重。
3. 最后对权重归一化。

SIS 算法会出现权值退化的情况，在一定时间后，可能会出现大部分权重都逼近0的情况，这是由于空间维度越来越高，需要的样本也越来越多。解决这个问题的方法有：

1. 重采样，以权重作为概率分布，重新在已经采样的样本中采样，然后所有样本的权重相同，这个方法的思路是将权重作为概率分布，然后得到累积密度函数，在累积密度上取点（阶梯函数）。
2. 选择一个合适的提议分布，\(q(z_t|z_{1:t-1},x_{1:t})=p(z_t|z_{t-1})\)，于是就消掉了一项，并且采样的概率就是 \(p(z_t|z_{t-1})\)，这就叫做生成与测试方法。

采用重采样的 SIS 算法就是基本的粒子滤波算法。如果像上面那样选择提议分布，这个算法叫做 SIR 算法。

条件随机场

我们知道，分类问题可以分为硬分类和软分类两种，其中硬分类有 SVM，PLA，LDA 等。软分类问题大体上可以分为概率生成和概率判别模型，其中较为有名的概率判别模型有 Logistic 回归，生成模型有朴素贝叶斯模型。Logistic 回归模型的损失函数为交叉熵，这类模型也叫对数线性模型，一般地，又叫做最大熵模型，这类模型和指数族分布的概率假设是一致的。对朴素贝叶斯假设，如果将其中的单元素的条件独立性做推广到一系列的隐变量，那么，由此得到的模型又被称为动态模型，比较有代表性的如 HMM，从概率意义上，HMM也可以看成是 GMM 在时序上面的推广。

我们看到，一般地，如果将最大熵模型和 HMM相结合，那么这种模型叫做最大熵 Markov 模型（MEMM）：

graph LR;
    x4((x4))-->y4
        x2((x2))-->y2
            x1((x1))-->y1
                x3((x3))-->y3
    y1-->y2;
    y2-->y3;
y3-->y4;

这个图就是将 HMM 的图中观测变量和隐变量的边方向反向，应用在分类中，隐变量就是输出的分类，这样 HMM 中的两个假设就不成立了，特别是观测之间不是完全独立的了。

HMM 是一种生成式模型，其建模对象为 \(p(X,Y|\lambda)\)，根据 HMM 的概率图，\(p(X,Y|\lambda)=\prod\limits_{t=1}^Tp(x_t,y_t|\lambda,y_{t-1})\)。我们看到，观测独立性假设是一个很强的假设，如果我们有一个文本样本，那么观测独立性假设就假定了所有的单词之间没有关联。

在 MEMM 中，建模对象是 \(p(Y|X,\lambda)\)，我们看概率图，给定 \(y_t\)，\(x_t,x_{t-1}\) 是不独立的，这样，观测独立假设就不成立了。根据概率图，\(p(Y|X,\lambda)=\prod\limits_{t=1}^Tp(y_t|y_{t-1},X,\lambda)\)。

MEMM 的缺陷是其必须满足局域的概率归一化（Label Bias Problem），我们看到，在上面的概率图中，\(p(y_t|y_{t-1},x_t)\)， 这个概率，如果 \(p(y_t|y_{t-1})\) 非常接近1，那么事实上，观测变量是什么就不会影响这个概率了。

对于这个问题，我们将 \(y\) 之间的箭头转为直线转为无向图（线性链条件随机场），这样就只要满足全局归一化了（破坏齐次 Markov 假设）。

graph LR;
    x4((x4))-->y4
        x2((x2))-->y2
            x1((x1))-->y1
                x3((x3))-->y3
    y1---y2;
    y2---y3;
y3---y4;

CRF 的 PDF

线性链的 CRF 的 PDF 为 \(p(Y|X)=\frac{1}{Z}\exp\sum\limits_{t=1}^T(F_t(y_{t-1},y_t,x_{1:T}))\)，两两形成了最大团，其中 \(y_0\) 是随意外加的一个元素。作为第一个简化，我们假设每个团的势函数相同 \(F_t=F\)。

对于这个 \(F\)，我们进一步，可以将其写为 $ F(y_{t-1},y_t,X)={y{t-1},X}+{y{t},X}+{y_t,y{t-1},X}$这三个部分，分别表示状态函数已经转移函数，由于整体的求和，可以简化为 $ F(y_{t-1},y_t,X)={y{t},X}+{y_t,y{t-1},X}$。

我们可以设计一个表达式将其参数化：
\[ \begin{align*} \Delta_{y_t,y_{t-1},X}&=\sum\limits_{k=1}^K\lambda_kf_k(y_{t-1},y_t,X)\\ \Delta_{y_{t},X}&=\sum\limits_{l=1}^L\eta_lg_l(y_t,X) \end{align*} \]
其中 $g,f $ 叫做特征函数，对于 \(y\) 有 \(S\) 种元素，那么 \(K\le S^2,L\le S\)。

代入概率密度函数中：
\[ p(Y|X)=\frac{1}{Z}\exp\sum\limits_{t=1}^T[\sum\limits_{k=1}^K\lambda_kf_k(y_{t-1},y_t,X)+\sum\limits_{l=1}^L\eta_lg_l(y_t,X)] \]
对于单个样本，将其写成向量的形式。定义 \(y=(y_1,y_2,\cdots,y_T)^T,x=(x_1,x_2,\cdots,x_T)^T,\lambda=(\lambda_1,\lambda_2,\cdots,\lambda_K)^T,\eta=(\eta_1,\eta_2,\cdots,\eta_L)^T\)。并且有 \(f=(f_1,f_2,\cdots,f_K)^T,g=(g_1,g_2,\cdots,g_L)^T\)。于是：
\[ p(Y=y|X=x)=\frac{1}{Z}\exp\sum\limits_{t=1}^T[\lambda^Tf(y_{t-1},y_t,x)+\eta^Tg(y_t,x)] \]
不妨记：\(\theta=(\lambda,\eta)^T,H=(\sum\limits_{t=1}^Tf,\sum\limits_{t=1}^Tg)^T\)：
\[ p(Y=y|X=x)=\frac{1}{Z(x,\theta)}\exp[\theta^TH(y_t,y_{t-1},x)] \]
上面这个式子是一个指数族分布，于是 \(Z\) 是配分函数。

CRF 需要解决下面几个问题：

1. Learning：参数估计问题，对 \(N\) 个 \(T\) 维样本，\(\hat{\theta}=\mathop{argmax}\limits_{\theta}\prod\limits_{i=1}^Np(y^i|x^i)\)，这里用上标表示样本的编号。

2. Inference：

   1. 边缘概率：
      \[ p(y_t|x) \]

3. 条件概率：一般在生成模型中较为关注，CRF 中不关注

4. MAP 推断：
   \[ \hat{y}=\mathop{argmax}p(y|x) \]

边缘概率

边缘概率这个问题描述为，根据学习任务得到的参数，给定了 \(p(Y=y|X=x)\)，求解 \(p(y_t=i|x)\)。根据无向图可以给出：
\[ p(y_t=i|x)=\sum\limits_{y_{1:t-1},y_{t+1:T}}p(y|x)=\sum\limits_{y_{1:t-1}}\sum\limits_{y_{t+1:T}}\frac{1}{Z}\prod\limits_{t'=1}^T\phi_{t'}(y_{t'-1},y_{t'},x) \]
我们看到上面的式子，直接计算的复杂度很高，这是由于求和的复杂度在 \(O(S^T)\)，求积的复杂度在 \(O(T)\)，所以整体复杂度为 \(O(TS^T)\)。我们需要调整求和符号的顺序，从而降低复杂度。

首先，将两个求和分为：
\[ \begin{align*}&p(y_t=i|x)=\frac{1}{Z}\Delta_l\Delta_r\\ &\Delta_l=\sum\limits_{y_{1:t-1}}\phi_{1}(y_0,y_1,x)\phi_2(y_1,y_2,x)\cdots\phi_{t-1}(y_{t-2},y_{t-1},x)\phi_t(y_{t-1},y_t=i,x)\\ &\Delta_r=\sum\limits_{y_{t+1:T}}\phi_{t+1}(y_t=i,y_{t+1},x)\phi_{t+2}(y_{t+1},y_{t+2},x)\cdots\phi_T(y_{T-1},y_T,x) \end{align*} \]
对于 \(\Delta_l\)，从左向右，一步一步将 \(y_t\) 消掉：
\[ \Delta_l=\sum\limits_{y_{t-1}}\phi_t(y_{t-1},y_t=i,x)\sum\limits_{y_{t-2}}\phi_{t-1}(y_{t-2},y_{t-1},x)\cdots\sum\limits_{y_0}\phi_1(y_0,y_1,x) \]
引入：
\[ \alpha_t(i)=\Delta_l \]
于是：
\[ \alpha_{t}(i)=\sum\limits_{j\in S}\phi_t(y_{t-1}=j,y_t=i,x)\alpha_{t-1}(j) \]
这样我们得到了一个递推式。

类似地，\(\Delta_r=\beta_t(i)=\sum\limits_{j\in S}\phi_{t+1}(y_t=i,y_{t+1}=j,x)\beta_{t+1}(j)\)。这个方法和 HMM 中的前向后向算法类似，就是概率图模型中精确推断的变量消除算法（信念传播）。

参数估计

在进行各种类型的推断之前，还需要对参数进行学习：
\[ \begin{align*}\hat{\theta}&=\mathop{argmax}_{\theta}\prod\limits_{i=1}^Np(y^i|x^i)\\ &=\mathop{argmax}_\theta\sum\limits_{i=1}^N\log p(y^i|x^i)\\ &=\mathop{argmax}_\theta\sum\limits_{i=1}^N[-\log Z(x^i,\lambda,\eta)+\sum\limits_{t=1}^T[\lambda^Tf(y_{t-1},y_t,x)+\eta^Tg(y_t,x)]] \end{align*} \]
上面的式子中，第一项是对数配分函数，根据指数族分布的结论：
\[ \nabla_\lambda(\log Z(x^i,\lambda,\eta))=\mathbb{E}_{p(y^i|x^i)}[\sum\limits_{t=1}^Tf(y_{t-1},y_t,x^i)] \]
其中，和 \(\eta\) 相关的项相当于一个常数。求解这个期望值：
\[ \mathbb{E}_{p(y^i|x^i)}[\sum\limits_{t=1}^Tf(y_{t-1},y_t,x^i)]=\sum\limits_{y}p(y|x^i)\sum\limits_{t=1}^Tf(y_{t-1},y_t,x^i) \]
第一个求和号的复杂度为 \(O(S^T)\)，重新排列求和符号：
\[ \begin{align*}\mathbb{E}_{p(y^i|x^i)}[\sum\limits_{t=1}^Tf(y_{t-1},y_t,x^i)]&=\sum\limits_{t=1}^T\sum\limits_{y_{1:t-2}}\sum\limits_{y_{t-1}}\sum\limits_{y_t}\sum\limits_{y_{t+1:T}}p(y|x^i)f(y_{t-1},y_t,x^i)\\ &=\sum\limits_{t=1}^T\sum\limits_{y_{t-1}}\sum\limits_{y_t}p(y_{t-1},y_t|x^i)f(y_{t-1},y_t,x^i) \end{align*} \]
和上面的边缘概率类似，也可以通过前向后向算法得到上面式子中的边缘概率。

于是：
\[ \nabla_\lambda L=\sum\limits_{i=1}^N\sum\limits_{t=1}^T[f(y_{t-1},y_t,x^i)-\sum\limits_{y_{t-1}}\sum\limits_{y_t}p(y_{t-1},y_t|x^i)f(y_{t-1},y_t,x^i)] \]
利用梯度上升算法可以求解。对于 \(\eta\) 也是类似的过程。

译码

译码问题和 HMM 中的 Viterbi 算法类似，同样采样动态规划的思想一层一层求解最大值。

高斯网络

高斯图模型（高斯网络）是一种随机变量为连续的有向或者无向图。有向图版本的高斯图是高斯贝叶斯网络，无向版本的叫高斯马尔可夫网络。

高斯网络的每一个节点都是高斯分布：\(\mathcal{N}(\mu_i,\Sigma_i)\)，于是所有节点的联合分布就是一个高斯分布，均值为 \(\mu\)，方差为 \(\Sigma\)。

对于边缘概率，我们有下面三个结论：

1. 对于方差矩阵，可以得到独立性条件：\(x_i\perp x_j\Leftrightarrow\sigma_{ij}=0\)，这个叫做全局独立性。

2. 我们看方差矩阵的逆（精度矩阵或信息矩阵）：\(\Lambda=\Sigma^{-1}=(\lambda_{ij})_{pp}\)，有定理：

   \(x_i\perp x_j|(X-\{x_i,x_j\})\Leftrightarrow\lambda_{ij}=0\)

   因此，我们使用精度矩阵来表示条件独立性。

3. 对于任意一个无向图中的节点 \(x_i\)，\(x_i|(X-x_i)\sim \mathcal{N}(\sum\limits_{j\ne i}\frac{\lambda_{ij}}{\lambda_{ii}}x_j,\lambda_{ii}^{-1})\)

   也就是其他所有分量的线性组合，即所有与它有链接的分量的线性组合。

高斯贝叶斯网络 GBN

高斯贝叶斯网络可以看成是 LDS 的一个推广，LDS 的假设是相邻时刻的变量之间的依赖关系，因此是一个局域模型，而高斯贝叶斯网络，每一个节点的父亲节点不一定只有一个，因此可以看成是一个全局的模型。根据有向图的因子分解：
\[ p(x)=\prod\limits_{i=1}^pp(x_i|x_{Parents(i)}) \]
对里面每一项，假设每一个特征是一维的，可以写成线性组合：
\[ p(x_i|x_{Parents(i)})=\mathcal{N}(x_i|\mu_i+W_i^Tx_{Parents(i)},\sigma^2_i) \]
将随机变量写成：
\[ x_i=\mu_i+\sum\limits_{j\in x_{Parents(i)}}w_{ij}(x_j-\mu_j)+\sigma_i\varepsilon_i,\varepsilon_i\sim \mathcal{N}(0,1) \]
写成矩阵形式，并且对 \(w\) 进行扩展：
\[ x-\mu=W(x-\mu)+S\varepsilon \]
其中，\(S=diag(\sigma_i)\)。所以有：\(x-\mu=(\mathbb{I}-W)^{-1}S\varepsilon\)

由于：
\[ Cov(x)=Cov(x-\mu) \]
可以得到协方差矩阵。

高斯马尔可夫网络 GMN

对于无向图版本的高斯网络，可以写成：
\[ p(x)=\frac{1}{Z}\prod\limits_{i=1}^p\phi_i(x_i)\prod\limits_{i,j\in X}\phi_{i,j}(x_i,x_j) \]
为了将高斯分布和这个式子结合，我们写出高斯分布和变量相关的部分：
\[ \begin{align*}p(x)&\propto \exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))\\ &=\exp(-\frac{1}{2}(x^T\Lambda x-2\mu^T\Lambda x+\mu^T\Lambda\mu))\\ &=\exp(-\frac{1}{2}x^T\Lambda x+(\Lambda\mu)^Tx) \end{align*} \]
可以看到，这个式子与无向图分解中的两个部分对应，我们记 \(h=\Lambda\mu\)为 Potential Vector。其中和 \(x_i\) 相关的为：\(x_i:-\frac{1}{2}\lambda_{ii}x_i^2+h_ix_i\)，与 \(x_i,x_j\) 相关的是：\(x_i,x_j:-\lambda_{ij}x_ix_j\)，这里利用了精度矩阵为对称矩阵的性质。我们看到，这里也可以看出，\(x_i,x_j\) 构成的一个势函数，只和 \(\lambda_{ij}\) 有关，于是 $x_ix_j|(X-{x_i,x_j})_{ij}=0 $。

贝叶斯线性回归

我们知道，线性回归当噪声为高斯分布的时候，最小二乘损失导出的结果相当于对概率模型应用 MLE，引入参数的先验时，先验分布是高斯分布，那么 MAP的结果相当于岭回归的正则化，如果先验是拉普拉斯分布，那么相当于 Lasso 的正则化。这两种方案都是点估计方法。我们希望利用贝叶斯方法来求解参数的后验分布。

线性回归的模型假设为：
\[ \begin{align*}f(x)=w^Tx \\y=f(x)+\varepsilon\\ \varepsilon\sim\mathcal{N}(0,\sigma^2) \end{align*} \]
在贝叶斯方法中，需要解决推断和预测两个问题。

推断

引入高斯先验：
\[ p(w)=\mathcal{N}(0,\Sigma_p) \]
对参数的后验分布进行推断：
\[ p(w|X,Y)=\frac{p(w,Y|X)}{p(Y|X)}=\frac{p(Y|w,X)p(w|X)}{\int p(Y|w,X)p(w|X)dw} \]
分母和参数无关，由于 \(p(w|X)=p(w)\)，代入先验得到：
\[ p(w|X,Y)\propto \prod\limits_{i=1}^N\mathcal{N}(y_i|w^Tx_i,\sigma^2)\cdot\mathcal{N}(0,\Sigma_p) \]
高斯分布取高斯先验的共轭分布依然是高斯分布，于是可以得到后验分布也是一个高斯分布。第一项：
\[ \begin{align*}\prod\limits_{i=1}^N\mathcal{N}(y_i|w^Tx_i,\sigma^2)&=\frac{1}{(2\pi)^{N/2}\sigma^N}\exp(-\frac{1}{2\sigma^2}\sum\limits_{i=1}^N(y_i-w^Tx_i)^2)\\ &=\frac{1}{(2\pi)^{N/2}\sigma^N}\exp(-\frac{1}{2}(Y-Xw)^T(\sigma^{-2}\mathbb{I})(Y-Xw)) \\&=\mathcal{N}(Xw,\sigma^2\mathbb{I}) \end{align*} \]
代入上面的式子：
\[ p(w|X,Y)\propto\exp(-\frac{1}{2\sigma^2}(Y-Xw)^T\sigma^{-2}\mathbb{I}(Y-Xw)-\frac{1}{2}w^T\Sigma_p^{-1}w) \]
假定最后得到的高斯分布为：\(\mathcal{N}(\mu_w,\Sigma_w)\)。对于上面的分布，采用配方的方式来得到最终的分布，指数上面的二次项为：
\[ -\frac{1}{2\sigma^2}w^TX^TXw-\frac{1}{2}w^T\Sigma_p^{-1}w \]
于是：
\[ \Sigma_w^{-1}=\sigma^{-2}X^TX+\Sigma_p^{-1}=A \]
一次项：
\[ \frac{1}{2\sigma^2}2Y^TXw=\sigma^{-2}Y^TXw \]
于是：
\[ \mu_w^T\Sigma_w^{-1}=\sigma^{-2}Y^TX\Rightarrow\mu_w=\sigma^{-2}A^{-1}X^TY \]

预测

给定一个 \(x^*\)，求解 \(y^*\)，所以 \(f(x^*)=x^{*T}w\)，代入参数后验，有 \(x^{*T}w\sim \mathcal{N}(x^{*T}\mu_w,x^{*T}\Sigma_wx^*)\)，添上噪声项：
\[ \begin{align*} p(y^*|X,Y,x^*)&=\int_wp(y^*|w,X,Y,x^*)p(w|X,Y,x^*)dw\\&=\int_wp(y^*|w,x^*)p(w|X,Y)dw\\ &=\mathcal{N}(x^{*T}\mu_w,x^{*T}\Sigma_wx^*+\sigma^2) \end{align*} \]

高斯过程回归

将一维高斯分布推广到多变量中就得到了高斯网络，将多变量推广到无限维，就得到了高斯过程，高斯过程是定义在连续域（时间空间）上的无限多个高维随机变量所组成的随机过程。

在时间轴上的任意一个点都满足高斯分布吗，将这些点的集合叫做高斯过程的一个样本。

对于时间轴上的序列 \(\xi_t\)，如果 \(\forall n\in N^+，t_i\in T\)，有 \(\xi_{t_1-t_n}\sim \mathcal{N}(\mu_{t_1-t_n},\Sigma_{t_1-t_n})\)， 那么 \(\{\xi_t\}_{t\in T}\) 是一个高斯过程。

高斯过程有两个参数（高斯过程存在性定理），均值函数 \(m(t)=\mathbb{E}[\xi_t]\) 和协方差函数 \(k(s,t)=\mathbb{E}[(\xi_s-\mathbb{E}[\xi_s])(\xi_t-\mathbb{E}[\xi_t])]\)。

我们将贝叶斯线性回归添加核技巧的这个模型叫做高斯过程回归，高斯过程回归分为两种视角：

1. 权空间的视角-核贝叶斯线性回归，相当于 \(x\) 为 \(t\)，在每个时刻的高斯分布来源于权重，根据上面的推导，预测的函数依然是高斯分布。
2. 函数空间的视角-高斯分布通过函数 \(f(x)\) 来体现。

核贝叶斯线性回归

贝叶斯线性回归可以通过加入核函数的方法来解决非线性函数的问题，将 \(f(x)=x^Tw\) 这个函数变为 \(f(x)=\phi(x)^Tw\)（当然这个时候，$ _p$ 也要变为更高维度的），变换到更高维的空间，有：
\[ \begin{align*}f(x^*)\sim \mathcal{N}(\phi(x^*)^{T}\sigma^{-2}A^{-1}\Phi^TY,\phi(x^*)^{T}A^{-1}\phi(x^*))\\ A=\sigma^{-2}\Phi^T\Phi+\Sigma_p^{-1} \end{align*} \]
其中，\(\Phi=(\phi(x_1),\phi(x_2),\cdots,\phi(x_N))^T\)。

为了求解 \(A^{-1}\)，可以利用 Woodbury Formula，\(A=\Sigma_p^{-1},C=\sigma^{-2}\mathbb{I}\)：
\[ (A+UCV)^{-1}=A^{-1}-A^{-1}U(C^{-1}+VA^{-1}U)^{-1}VA^{-1} \]
所以 \(A^{-1}=\Sigma_p-\Sigma_p\Phi^T(\sigma^2\mathbb{I}+\Phi\Sigma_p\Phi^T)^{-1}\Phi\Sigma_p\)

也可以用另一种方法：
\[ \begin{align*} A&=\sigma^{-2}\Phi^T\Phi+\Sigma_p^{-1}\\ \Leftrightarrow A\Sigma_p&=\sigma^{-2}\Phi^T\Phi\Sigma_p+\mathbb{I}\\ \Leftrightarrow A\Sigma_p\Phi^T&=\sigma^{-2}\Phi^T\Phi\Sigma_p\Phi^T+\Phi^T=\sigma^{-2}\Phi^T(k+\sigma^2\mathbb{I})\\ \Leftrightarrow \Sigma_p\Phi^T&=\sigma^{-2}A^{-1}\Phi^T(k+\sigma^2\mathbb{I})\\ \Leftrightarrow \sigma^{-2}A^{-1}\Phi^T&=\Sigma_p\Phi^T(k+\sigma^2\mathbb{I})^{-1}\\ \Leftrightarrow \phi(x^*)^T\sigma^{-2}A^{-1}\Phi^T&=\phi(x^*)^T\Sigma_p\Phi^T(k+\sigma^2\mathbb{I})^{-1} \end{align*} \]
上面的左边的式子就是变换后的均值，而右边的式子就是不含 \(A^{-1}\) 的式子，其中 \(k=\Phi\Sigma_p\Phi^T\)。

根据 \(A^{-1}\) 得到方差为：
\[ \phi(x^*)^T\Sigma_p\phi(x^*)-\phi(x^*)^T\Sigma_p\Phi^T(\sigma^2\mathbb{I}+k)^{-1}\Phi\Sigma_p\phi(x^*) \]
上面定义了：
\[ k=\Phi\Sigma_p\Phi^T \]
我们看到，在均值和方差中，含有下面四项：
\[ \phi(x^*)^T\Sigma_p\Phi^T,\phi(x^*)^T\Sigma_p\phi(x^*),\phi(x^*)^T\Sigma_p\Phi^T,\Phi\Sigma_p\phi(x^*) \]
展开后，可以看到，有共同的项：\(k(x,x')=\phi(x)^T\Sigma_p\phi(x‘)\)。由于 \(\Sigma_p\) 是正定对称的方差矩阵，所以，这是一个核函数。

对于高斯过程中的协方差：
\[ k(t,s)=Cov[f(x),f(x')]=\mathbb{E}[\phi(x)^Tww^T\phi(x')]=\phi(x)^T\mathbb{E}[ww^T]\phi(x')=\phi(x)^T\Sigma_p\phi(x') \]
我们可以看到，这个就对应着上面的核函数。因此我们看到 \(\{f(x)\}\) 组成的组合就是一个高斯过程。

函数空间的观点

相比权重空间，我们也可以直接关注 \(f\) 这个空间，对于预测任务，这就是类似于求：
\[ p(y^*|X,Y,x^*)=\int_fp(y^*|f,X,Y,x^*)p(f|X,Y,x^*)df \]
对于数据集来说，取 \(f(X)\sim\mathcal{N}(\mu(X),k(X,X)),Y=f(X)+\varepsilon\sim\mathcal{N}(\mu(X),k(X,X)+\sigma^2\mathbb{I})\)。预测任务的目的是给定一个新数据序列 \(X^*=(x_1^*,\cdots,x_M^*)^T\)，得到 \(Y^*=f(X^*)+\varepsilon\)。我们可以写出：
\[ \begin{pmatrix}Y\\f(X^*)\end{pmatrix}\sim\mathcal{N}\left(\begin{pmatrix}\mu(X)\\\mu(X^*)\end{pmatrix},\begin{pmatrix}k(X,X)+\sigma^2\mathbb{I}&k(X,X^*)\\k(X^*,X)&k(X^*,X^*)\end{pmatrix}\right) \]
根据高斯分布的方法：
\[ \begin{align*}x=\begin{pmatrix}x_a\\x_b\end{pmatrix}\sim\mathcal{N}\left(\begin{pmatrix}\mu_a\\\mu_b\end{pmatrix},\begin{pmatrix}\Sigma_{aa}&\Sigma_{ab}\\\Sigma_{ba}&\Sigma_{bb}\end{pmatrix}\right)\\ x_b|x_a\sim\mathcal{N}(\mu_{b|a},\Sigma_{b|a})\\ \mu_{b|a}=\Sigma_{ba}\Sigma_{aa}^{-1}(x_a-\mu_a)+\mu_b\\ \Sigma_{b|a}=\Sigma_{bb}-\Sigma_{ba}\Sigma_{aa}^{-1}\Sigma_{ab} \end{align*} \]
可以直接写出：
\[ \begin{gather*} p(f(X^*)|X,Y,X^*)=p(f(X^*)|Y)\\ =\mathcal{N}(k(X^*,X)[k(X,X)+\sigma^2\mathbb{I}]^{-1}(Y-\mu(X))+\mu(X^*),\\ k(X^*,X^*)-k(X^*,X)[k(X,X)+\sigma^2\mathbb{I}]^{1}k(X,X^*)) \end{gather*} \]
所以对于 \(Y=f(X^*)+\varepsilon\)：
\[ \begin{gather*} \mathcal{N}(k(X^*,X)[k(X,X)+\sigma^2\mathbb{I}]^{-1}(Y-\mu(X))+\mu(X^*),\\ k(X^*,X^*)-k(X^*,X)[k(X,X)+\sigma^2\mathbb{I}]^{1}k(X,X^*)+\sigma^2\mathbb{I}) \end{gather*} \]
我们看到，函数空间的观点更加简单易于求解。

受限玻尔兹曼机

玻尔兹曼机是一种存在隐节点的无向图模型。在图模型中最简单的是朴素贝叶斯模型（朴素贝叶斯假设），引入单个隐变量后，发展出了 GMM，如果单个隐变量变成序列的隐变量，就得到了状态空间模型（引入齐次马尔可夫假设和观测独立假设就有HMM，Kalman Filter，Particle Filter），为了引入观测变量之间的关联，引入了一种最大熵模型-MEMM，为了克服 MEMM 中的局域问题，又引入了 CRF，CRF 是一个无向图，其中，破坏了齐次马尔可夫假设，如果隐变量是一个链式结构，那么又叫线性链 CRF。

在无向图的基础上，引入隐变量得到了玻尔兹曼机，这个图模型的概率密度函数是一个指数族分布。对隐变量和观测变量作出一定的限制，就得到了受限玻尔兹曼机（RBM）。

我们看到，不同的概率图模型对下面几个特点作出假设：

1. 方向-边的性质
2. 离散/连续/混合-点的性质
3. 条件独立性-边的性质
4. 隐变量-节点的性质
5. 指数族-结构特点

将观测变量和隐变量分别记为 \(v,h,h=\{h_1,\cdots,h_m\},v=\{v_1,\cdots,v_n\}\)。我们知道，无向图根据最大团的分解，可以写为玻尔兹曼分布的形式 \(p(x)=\frac{1}{Z}\prod\limits_{i=1}^K\psi_i(x_{ci})=\frac{1}{Z}\exp(-\sum\limits_{i=1}^KE(x_{ci}))\)，这也是一个指数族分布。

一个玻尔兹曼机存在一系列的问题，在其推断任务中，想要精确推断，是无法进行的，想要近似推断，计算量过大。为了解决这个问题，一种简化的玻尔兹曼机-受限玻尔兹曼机作出了假设，所有隐变量内部以及观测变量内部没有连接，只在隐变量和观测变量之间有连接，这样一来：
\[ p(x)=p(h,v)=\frac{1}{Z}\exp(-E(v,h)) \]
其中能量函数 \(E(v,h)\) 可以写出三个部分，包括与节点集合相关的两项以及与边 \(w\) 相关的一项，记为：
\[ E(v,h)=-(h^Twv+\alpha^T v+\beta^T h) \]
所以：
\[ p(x)=\frac{1}{Z}\exp(h^Twv)\exp(\alpha^T v)\exp(\beta^T h)=\frac{1}{Z}\prod_{i=1}^m\prod_{j=1}^n\exp(h_iw_{ij}v_j)\prod_{j=1}^n\exp(\alpha_jv_j)\prod_{i=1}^m\exp(\beta_ih_i) \]
上面这个式子也和 RBM 的因子图一一对应。

推断

推断任务包括求后验概率 $ p(v|h),p(h|v)$ 以及求边缘概率 \(p(v)\)。

\(p(h|v)\)

对于一个无向图，满足局域的 Markov 性质，即 \(p(h_1|h-\{h_1\},v)=p(h_1|Neighbour(h_1))=p(h_1|v)\)。我们可以得到：
\[ p(h|v)=\prod_{i=1}^mp(h_i|v) \]
考虑 Binary RBM，所有的隐变量只有两个取值 \(0,1\)：
\[ p(h_l=1|v)=\frac{p(h_l=1,h_{-l},v)}{p(h_{-l},v)}=\frac{p(h_l=1,h_{-l},v)}{p(h_l=1,h_{-l},v)+p(h_l=0,h_{-l},v)} \]
将能量函数写成和 \(l\) 相关或不相关的两项：
\[ E(v,h)=-(\sum\limits_{i=1,i\ne l}^m\sum\limits_{j=1}^nh_iw_{ij}v_j+h_l\sum\limits_{j=1}^nw_{lj}v_j+\sum\limits_{j=1}^n\alpha_j v_j+\sum\limits_{i=1,i\ne l}^m\beta_ih_i+\beta_lh_l) \]
定义：\(h_lH_l(v)=h_l\sum\limits_{j=1}^nw_{lj}v_j+\beta_lh_l,\overline{H}(h_{-l},v)=\sum\limits_{i=1,i\ne l}^m\sum\limits_{j=1}^nh_iw_{ij}v_j+\sum\limits_{j=1}^n\alpha_j v_j+\sum\limits_{i=1,i\ne l}^m\beta_ih_i\)。

代入，有：
\[ p(h_l=1|v)=\frac{\exp(H_l(v)+\overline{H}(h_{-l},v))}{\exp(H_l(v)+\overline{H}(h_{-l},v))+\exp(\overline{H}(h_{-l},v))}=\frac{1}{1+\exp(-H_l(v))}=\sigma(H_l(v)) \]
于是就得到了后验概率。对于 \(v\) 的后验是对称的，所以类似的可以求解。

\(p(v)\)

\[ \begin{align*}p(v)&=\sum\limits_hp(h,v)=\sum\limits_h\frac{1}{Z}\exp(h^Twv+\alpha^Tv+\beta^Th)\\ &=\exp(\alpha^Tv)\frac{1}{Z}\sum\limits_{h_1}\exp(h_1w_1v+\beta_1h_1)\cdots\sum\limits_{h_m}\exp(h_mw_mv+\beta_mh_m)\\ &=\exp(\alpha^Tv)\frac{1}{Z}(1+\exp(w_1v+\beta_1))\cdots(1+\exp(w_mv+\beta_m))\\ &=\frac{1}{Z}\exp(\alpha^Tv+\sum\limits_{i=1}^m\log(1+\exp(w_iv+\beta_i))) \end{align*} \]

其中，\(\log(1+\exp(x))\) 叫做 Softplus 函数。

谱聚类

聚类问题可以分为两种思路：

1. Compactness，这类有 K-means，GMM 等，但是这类算法只能处理凸集，为了处理非凸的样本集，必须引入核技巧。
2. Connectivity，这类以谱聚类为代表。

谱聚类是一种基于无向带权图的聚类方法。这个图用 \(G=(V,E)\) 表示，其中 \(V=\{1,2,\cdots,N\}\)，\(E=\{w_{ij}\}\)，这里 \(w_{ij}\) 就是边的权重，这里权重取为相似度，\(W=(w_{ij})\) 是相似度矩阵，定义相似度（径向核）：
\[ \begin{gather*} w_{ij}=k(x_i,x_j)=\exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2}),(i,j)\in E\\ w_{ij}=0,(i,j)\notin E \end{gather*} \]
下面定义图的分割，这种分割就相当于聚类的结果。定义 \(w(A,B)\)：
\[ A\subset V,B\subset V,A\cap B=\emptyset,w(A,B)=\sum\limits_{i\in A,j\in B}w_{ij} \]
假设一共有 \(K\) 个类别，对这个图的分割 \(CUT(V)=CUT(A_1,A_2,\cdots,A_K)=\sum\limits_{k=1}^Kw(A_k,\overline{A_k})=\sum\limits_{k=1}^K[w(A_k,V)-w(A_k,A_k)]\)

于是，我们的目标就是 \(\min\limits_{A_k}CUT(V)\)。

为了平衡每一类内部的权重不同，我们做归一化的操作，定义每一个集合的度，首先，对单个节点的度定义：
\[ d_i=\sum\limits_{j=1}^Nw_{ij} \]
其次，每个集合：
\[ \Delta_k=degree(A_k)=\sum\limits_{i\in A_k}d_i \]
于是：
\[ N(CUT)=\sum\limits_{k=1}^K\frac{w(A_k,\overline{A_k})}{\sum\limits_{i\in A_k}d_i} \]
所以目标函数就是最小化这个式子。

谱聚类的模型就是：
\[ \{\hat{A}_k\}_{k=1}^K=\mathop{argmin}_{A_k}N(CUT) \]
引入指示向量：
\[ \left\{ \begin{align*}y_i\in \{0,1\}^K\\ \sum\limits_{j=1}^Ky_{ij}=1\end{align*} \right. \]
其中，\(y_{ij}\) 表示第 \(i\) 个样本属于 \(j\) 个类别，记：\(Y=(y_1,y_2,\cdots,y_N)^T\)。所以：
\[ \hat{Y}=\mathop{argmin}_YN(CUT) \]
将 \(N(CUT)\) 写成对角矩阵的形式，于是：
\[ \begin{align*}N(CUT)&=Trace[diag(\frac{w(A_1,\overline{A_1})}{\sum\limits_{i\in A_1}d_i},\frac{w(A_2,\overline{A_2})}{\sum\limits_{i\in A_2}d_i},\cdots,\frac{w(A_K,\overline{A_K})}{\sum\limits_{i\in A_K}d_i})]\\ &=Trace[diag(w(A_1,\overline{A_1}),w(A_2,\overline{A_2}),\cdots,w(A_K,\overline{A_K}))\cdot diag(\sum\limits_{i\in A_1}d_i,\cdots,\sum\limits_{i\in A_K}d_i)^{-1}]\\ &=Trace[O\cdot P^{-1}] \end{align*} \]
我们已经知道 \(Y,w\) 这两个矩阵，我们希望求得 \(O,P\)。

由于：
\[ Y^TY=\sum\limits_{i=1}^Ny_iy_i^T \]
对于 \(y_iy_i^T\)，只在对角线上的 \(k\times k\) 处为 1，所以：
\[ Y^TY=diag(N_1,N_2,\cdots,N_K) \]
其中，\(N_i\) 表示有 \(N_i\) 个样本属于 \(i\)，即 \(N_k=\sum\limits_{k\in A_k}1\)。

引入对角矩阵，根据 \(d_i\) 的定义， \(D=diag(d_1,d_2,\cdots,d_N)=diag(w_{NN}\mathbb{I}_{N1})\)，于是：
\[ P=Y^TDY \]
对另一项 \(O=diag(w(A_1,\overline{A_1}),w(A_2,\overline{A_2}),\cdots,w(A_K,\overline{A_K})\)：
\[ O=diag(w(A_i,V))-diag(w(A_i,A_i))=diag(\sum\limits_{j\in A_i}d_j)-diag(w(A_i,A_i)) \]
其中，第一项已知，第二项可以写成 \(Y^TwY\)，这是由于：
\[ Y^TwY=\sum\limits_{i=1}^N\sum\limits_{j=1}^Ny_iy_j^Tw_{ij} \]
于是这个矩阵的第 \(lm\) 项可以写为：
\[ \sum\limits_{i\in A_l,j\in A_m}w_{ij} \]
这个矩阵的对角线上的项和 \(w(A_i,A_i)\) 相同，所以取迹后的取值不会变化。

所以：
\[ N(CUT)=Trace[(Y^T(D-w))Y)\cdot(Y^TDY)^{-1}] \]
其中，$ L=D-w$ 叫做拉普拉斯矩阵。

前馈神经网络

机器学习我们已经知道可以分为两大流派：

1. 频率派，这个流派的方法叫做统计学习，根据具体问题有下面的算法：

   1. 正则化，L1，L2 等

   2. 核化，如核支撑向量机

   3. 集成化，AdaBoost，RandomForest

   4. 层次化，神经网络，神经网络有各种不同的模型，有代表性的有：

      1. 多层感知机
      2. Autoencoder
      3. CNN
      4. RNN

      这几种模型又叫做深度神经网络。

2. 贝叶斯派，这个流派的方法叫概率图模型，根据图特点分为：

   1. 有向图-贝叶斯网络，加入层次化后有深度有向网络，包括
      1. Sigmoid Belief Network
      2. Variational Autoencoder
      3. GAN
   2. 无向图-马尔可夫网络，加入层次化后有深度玻尔兹曼机。
   3. 混合，加入层次化后有深度信念网络

   这几个加入层次化后的模型叫做深度生成网络。

从广义来说，深度学习包括深度生成网络和深度神经网络。

From PLA to DL

• 1958，PLA
• 1969，PLA 不能解决 XOR 等非线性数据
• 1981，MLP，多层感知机的出现解决了上面的问题
• 1986，BP 算法应用在 MLP 上，RNN
• 1989，CNN，Univeral Approximation Theorem，但是于此同时，由于深度和宽度的相对效率不知道，并且无法解决 BP 算法的梯度消失问题
• 1993，1995，SVM + kernel，AdaBoost，RandomForest，这些算法的发展，DL 逐渐没落
• 1997，LSTM
• 2006，基于 RBM 的 深度信念网络和深度自编码
• 2009，GPU的发展
• 2011，在语音方面的应用
• 2012，ImageNet
• 2013，VAE
• 2014，GAN
• 2016，AlphaGo
• 2018，GNN

DL 不是一个新的东西，其近年来的大发展主要原因如下：

1. 数据量变大
2. 分布式计算的发展
3. 硬件算力的发展

非线性问题

对于非线性的问题，有三种方法：

1. 非线性转换，将低维空间转换到高维空间（Cover 定理），从而变为一个线性问题。
2. 核方法，由于非线性转换是变换为高维空间，因此可能导致维度灾难，并且可能很难得到这个变换函数，核方法不直接寻找这个转换，而是寻找一个内积。
3. 神经网络方法，将复合运算变为基本的线性运算的组合。

配分函数

在学习和推断中，对于一个概率的归一化因子很难处理，这个归一化因子和配分函数相关。假设一个概率分布：
\[ p(x|\theta)=\frac{1}{Z(\theta)}\hat{p}(x|\theta),Z(\theta)=\int\hat{p}(x|\theta)dx \]

包含配分函数的 MLE

在学习任务中，采用最大似然：
\[ \begin{align*} \hat{\theta}&=\mathop{argmax}_{\theta}p(x|\theta)=\mathop{argmax}_\theta\sum\limits_{i=1}^N\log p(x_i|\theta)\\ &=\mathop{argmax}_\theta\sum\limits_{i=1}^N\log \hat{p}(x|\theta)-N\log Z(\theta)\\ &=\mathop{argmax}_{\theta}\frac{1}{N}\sum\limits_{i=1}^N\log \hat{p}(x|\theta)-\log Z(\theta)=\mathop{argmax}_\theta l(\theta) \end{align*} \]
求导：
\[ \begin{align*}\nabla_\theta\log Z(\theta)&=\frac{1}{Z(\theta)}\nabla_\theta Z(\theta)\\ &=\frac{p(x|\theta)}{\hat{p}(x|\theta)}\int\nabla_\theta \hat{p}(x|\theta)dx\\ &=\int\frac{p(x|\theta)}{\hat{p}(x|\theta)}\nabla_\theta\hat{p}(x|\theta)dx\\ &=\mathbb{E}_{p(x|\theta)}[\nabla_\theta\log\hat{p}(x|\theta)] \end{align*} \]
由于这个表达式和未知的概率相关，于是无法直接精确求解，需要近似采样，如果没有这一项，那么可以采用梯度下降，但是存在配分函数就无法直接采用梯度下降了。

上面这个期望值，是对模型假设的概率分布，定义真实概率分布为 \(p_{data}\)，于是，\(l(\theta)\) 中的第一项的梯度可以看成是从这个概率分布中采样出来的 \(N\) 个点求和平均，可以近似期望值。
\[ \nabla_\theta l(\theta)=\mathbb{E}_{p_{data}}[\nabla_\theta\log\hat{p}(x|\theta)]-\mathbb{E}_{p(x|\theta)}[\nabla_\theta\log\hat{p}(x|\theta)] \]
于是，相当于真实分布和模型假设越接近越好。上面这个式子第一项叫做正相，第二项叫做负相。为了得到负相的值，需要采用各种采样方法，如 MCMC。

采样得到 \(\hat{x}_{1-m}\sim p_{model}(x|\theta^t)\)，那么：
\[ \theta^{t+1}=\theta^t+\eta(\sum\limits_{i=1}^m\nabla_\theta \log \hat{p}(x_i|\theta^t)-\sum\limits_{i=1}^m\nabla_\theta\log \hat{p}(\hat{x_i}|\theta^t)) \]
这个算法也叫做基于 MCMC 采样的梯度上升。每次通过采样得到的样本叫做幻想粒子，如果这些幻想粒子区域的概率高于实际分布，那么最大化参数的结果就是降低这些部分的概率。

对比散度-CD Learning

上面对于负相的采样，最大的问题是，采样到达平稳分布的步骤数量是未知的。对比散度的方法，是对上述的采样是的初始值作出限制，直接采样 \(\hat{x}_i=x_i\)，这样可以缩短采样的混合时间。这个算法叫做 CD-k 算法，\(k\) 就是初始化后进行的演化时间，很多时候，即使 \(k=1\) 也是可以的。

我们看 MLE 的表达式：
\[ \begin{align*}\hat{\theta}&=\mathop{argmax}_{\theta}p(x|\theta)=\mathop{argmax}_{\theta}\frac{1}{N}\sum\limits_{i=1}^N\log p(x_i|\theta)=\mathbb{E}_{p_{data}}[\log p_{model}(x|\theta)]\\ &=\mathop{argmax}_\theta\int p_{data}\log p_{model}dx\\ &=\mathop{argmax}_\theta\int p_{data}\log \frac{p_{model}}{p_{data}}dx\\ &=\mathop{argmin}_\theta KL(p_{data}||p_{model}) \end{align*} \]
对于 CD-k 的采样过程，可以将初始值这些点表示为：
\[ p^0=p_{data} \]
而我们的模型需要采样过程达到平稳分布：
\[ p^\infty=p_{model} \]
因此，我们需要的是 \(KL(p^0||p^\infty)\)。定义 CD：
\[ KL(p^0||p^\infty)-KL(p^k||p^\infty) \]
这就是 CD-k 算法第 \(k\) 次采样的目标函数。

RBM 的学习问题

RBM 的参数为：
\[ \begin{align*} h=(h_1,\cdots,h_m)^T\\ v=(v_1,\cdots,v_n)^T\\ w=(w_{ij})_{mn}\\ \alpha=(\alpha_1,\cdots,\alpha_n)^T\\ \beta=(\beta_1,\cdots,\beta_m)^T \end{align*} \]
学习问题关注的概率分布为：
\[ \begin{align*} \log p(v)&=\log\sum\limits_{h}p(h,v)\\ &=\log\sum\limits_h\frac{1}{Z}\exp(-E(v,h))\\ &=\log\sum\limits_{h}\exp(-E(v,h))-\log\sum\limits_{v,h}\exp(-E(h,v)) \end{align*} \]
对上面这个式子求导第一项：
\[ \begin{align*} \frac{\partial \log\sum\limits_{h}\exp(-E(v,h))}{\partial\theta}&=-\frac{\sum\limits_h\exp(-E(v,h))\frac{\partial E(v,h)}{\partial\theta}}{\sum\limits_{h}\exp(-E(v,h))}\\ &=-\sum\limits_h\frac{\exp(-E(v,h))\frac{\partial E(v,h)}{\partial\theta}}{\sum\limits_{h}\exp(-E(v,h))}\\&=-\sum\limits_hp(h|v)\frac{\partial E(v,h)}{\partial\theta} \end{align*} \]
第二项：
\[ \frac{\partial \log\sum\limits_{v,h}\exp(-E(h,v))}{\partial\theta}=-\sum\limits_{h,v}\frac{\exp(-E(v,h))\frac{\partial E(v,h)}{\partial\theta}}{\sum\limits_{h,v}\exp(-E(v,h))}=-\sum\limits_{v,h}p(v,h)\frac{\partial E(v,h)}{\partial\theta} \]
所以有：
\[ \frac{\partial}{\partial\theta}\log p(v)=-\sum\limits_hp(h|v)\frac{\partial E(v,h)}{\partial\theta}+\sum\limits_{v,h}p(v,h)\frac{\partial E(v,h)}{\partial\theta} \]
将 RBM 的模型假设代入：
\[ E(v,h)=-(h^Twv+\alpha^Tv+\beta^Th) \]

1. \(w_{ij}\)：
   \[ \frac{\partial}{\partial w_{ij}}E(v,h)=-h_iv_j \]
   于是：
   \[ \frac{\partial}{\partial\theta}\log p(v)=\sum\limits_{h}p(h|v)h_iv_j-\sum\limits_{h,v}p(h,v)h_iv_j \]
   第一项：
   \[ \sum\limits_{h_1,h_2,\cdots,h_m}p(h_1,h_2,\cdots,h_m|v)h_iv_j=\sum\limits_{h_i}p(h_i|v)h_iv_j=p(h_i=1|v)v_j \]
   这里假设了 \(h_i\) 是二元变量。

   第二项：
   \[ \sum\limits_{h,v}p(h,v)h_iv_j=\sum\limits_{h,v}p(v)p(h|v)h_iv_j=\sum\limits_vp(v)p(h_i=1|v)v_j \]
   这个求和是指数阶的，于是需要采样解决，我么使用 CD-k 方法。

   对于第一项，可以直接使用训练样本得到，第二项采用 CD-k 采样方法，首先使用样本 \(v^0=v\)，然后采样得到 \(h^0\)，然后采样得到 \(v^1\)，这样顺次进行，最终得到 \(v^k\)，对于每个样本都得到一个 \(v^k\)，最终采样得到 \(N\) 个 $v^k $，于是第二项就是：
   \[ p(h_i=1|v^k)v_j^k \]
   具体的算法为：

   1. 对每一个样本中的 \(v\)，进行采样：
      1. 使用这个样本初始化采样
      2. 进行 \(k\) 次采样（0-k-1）：
         1. \(h_i^l\sim p(h_i|v^l)\)
         2. \(v_i^{l+1}\sim p(v_i|h^l)\)
      3. 将这些采样出来的结果累加进梯度中
   2. 重复进行上述过程，最终的梯度除以 \(N\)

近似推断

这一讲中的近似推断具体描述在深度生成模型中的近似推断。推断的目的有下面几个部分：

1. 推断本身，根据结果（观测）得到原因（隐变量）。
2. 为参数的学习提供帮助。

但是推断本身是一个困难的额任务，计算复杂度往往很高，对于无向图，由于节点之间的联系过多，那么因子分解很难进行，并且相互之间都有耦合，于是很难求解，仅仅在某些情况如 RBM 中可解，在有向图中，常常由于条件独立性问题，如两个节点之间条件相关（explain away），于是求解这些节点的条件概率就很困难，仅仅在某些概率假设情况下可解如高斯模型，于是需要近似推断。

事实上，我们常常讲推断问题变为优化问题，即：
\[ Log-likehood:\sum\limits_{v\in V}\log p(v) \]
对上面这个问题，由于：
\[ \log p(v)=\log\frac{p(v,h)}{p(h|v)}=\log\frac{p(v,h)}{q(h|v)}+\log\frac{q(h|v)}{p(h|v)} \]
左右两边对 \(h\) 积分：
\[ \int_h\log p(v)\cdot q(h|v)dh=\log p(v) \]
右边积分有：
\[ \mathbb{E}_{q(h|v)}[\log\frac{p(v,h)}{q(h|v)}]+KL(q(h|v)||p(h|v))=\mathbb{E}_{q(h|v)}[\log p(v,h)]+H(q)+KL(q||p) \]
其中前两项是 ELBO，于是这就变成一个优化 ELBO 的问题。

总结

Math

1. MLE
   \[ \theta_{MLE}=\mathop{argmax}\limits _{\theta}\log p(X|\theta)\mathop{=}\limits _{iid}\mathop{argmax}\limits _{\theta}\sum\limits _{i=1}^{N}\log p(x_{i}|\theta) \]

2. MAP
   \[ \theta_{MAP}=\mathop{argmax}\limits _{\theta}p(\theta|X)=\mathop{argmax}\limits _{\theta}p(X|\theta)\cdot p(\theta) \]

3. Gaussian Distribution
   \[ \begin{align*}&p(x|\mu,\Sigma)=\frac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}e^{-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu)}\\ &\Delta=(x-\mu)^{T}\Sigma^{-1}(x-\mu)=\sum\limits _{i=1}^{p}(x-\mu)^{T}u_{i}\frac{1}{\lambda_{i}}u_{i}^{T}(x-\mu)=\sum\limits _{i=1}^{p}\frac{y_{i}^{2}}{\lambda_{i}} \end{align*} \]

4. 已知 \(x\sim\mathcal{N}(\mu,\Sigma), y\sim Ax+b\)，有：
   \[ \begin{align*}y\sim\mathcal{N}(A\mu+b, A\Sigma A^T) \end{align*} \]

5. 记 \(x=(x_1, x_2,\cdots,x_p)^T=(x_{a,m\times 1}, x_{b,n\times1})^T,\mu=(\mu_{a,m\times1}, \mu_{b,n\times1}),\Sigma=\begin{pmatrix}\Sigma_{aa}&\Sigma_{ab}\\\Sigma_{ba}&\Sigma_{bb}\end{pmatrix}\)，已知 \(x\sim\mathcal{N}(\mu,\Sigma)\)，则：
   \[ \begin{align*}&x_a\sim\mathcal{N}(\mu_a,\Sigma_{aa})\\ &x_b|x_a\sim\mathcal{N}(\mu_{b|a},\Sigma_{b|a})\\ &\mu_{b|a}=\Sigma_{ba}\Sigma_{aa}^{-1}(x_a-\mu_a)+\mu_b\\ &\Sigma_{b|a}=\Sigma_{bb}-\Sigma_{ba}\Sigma_{aa}^{-1}\Sigma_{ab} \end{align*} \]

Linear Regression

Model

1. Dataset:
   \[ \mathcal{D}=\{(x_1, y_1),(x_2, y_2),\cdots,(x_N, y_N)\} \]

2. Notation:
   \[ X=(x_1,x_2,\cdots,x_N)^T,Y=(y_1,y_2,\cdots,y_N)^T \]

3. Model:
   \[ f(w)=w^Tx \]

Loss Function

1. 最小二乘误差/高斯噪声的MLE
   \[ L(w)=\sum\limits_{i=1}^N||w^Tx_i-y_i||^2_2 \]

闭式解

\[ \begin{align*}\hat{w}=(X^TX)^{-1}X^TY=X^+Y\\ X=U\Sigma V^T\\ X^+=V\Sigma^{-1}U^T \end{align*} \]

正则化

\[ \begin{align*} L1-Gaussian \ priori&:\mathop{argmin}\limits_wL(w)+\lambda||w||_1,\lambda\gt0\\ L2-Laplasian\ priori-Sparsity&:\mathop{argmin}\limits_wL(w)+\lambda||w||^2_2,\lambda \gt 0 \end{align*} \]

Linear Classification

Hard

PCA

1. Idea: 在线性模型上加入激活函数

2. Loss Function:

\[ L(w)=\sum\limits_{x_i\in\mathcal{D}_{wrong}}-y_iw^Tx_i \]

3. Parameters:

\[ w^{t+1}\leftarrow w^{t}+\lambda y_ix_i \]

Fisher

1. Idea: 投影，类内小，类间大。

2. Loss Function:
   \[ \begin{align*}&J(w)=\frac{w^TS_bw}{w^TS_ww}\\ &S_b=(\overline{x_{c1}}-\overline{x_{c2}})(\overline{x_{c1}}-\overline{x_{c2}})^T\\ &S_w=S_1+S_2 \end{align*} \]

3. 闭式解，投影方向:
   \[ S_w^{-1}(\overline{x_{c1}}-\overline{x_{c2}}) \]

Soft

判别模型

Logistic Regression

1. Idea，激活函数:
   \[ \begin{align*}p(C_1|x)&=\frac{1}{1+\exp(-a)}\\ a&=w^Tx \end{align*} \]

2. Loss Function(交叉熵):
   \[ \hat{w}=\mathop{argmax}_wJ(w)=\mathop{argmax}_w\sum\limits_{i=1}^N(y_i\log p_1+(1-y_i)\log p_0) \]

3. 解法，SGD
   \[ J'(w)=\sum\limits_{i=1}^N(y_i-p_1)x_i \]

生成模型

GDA

1. Model

   1. \(y\sim Bernoulli(\phi)\)
   2. \(x|y=1\sim\mathcal{N}(\mu_1,\Sigma)\)
   3. \(x|y=0\sim\mathcal{N}(\mu_0,\Sigma)\)

2. MAP
   \[ \begin{align*} &\mathop{argmax}_{\phi,\mu_0,\mu_1,\Sigma}\log p(X|Y)p(Y)\\ &=\mathop{argmax}_{\phi,\mu_0,\mu_1,\Sigma}\sum\limits_{i=1}^N((1-y_i)\log\mathcal{N}(\mu_0,\Sigma)+y_i\log \mathcal{N}(\mu_1,\Sigma)+y_i\log\phi+(1-y_i)\log(1-\phi)) \end{align*} \]

3. 解
   \[ \begin{align*}\phi&=\frac{N_1}{N}\\ \mu_1&=\frac{\sum\limits_{i=1}^Ny_ix_i}{N_1}\\ \mu_0&=\frac{\sum\limits_{i=1}^N(1-y_i)x_i}{N_0}\\ \Sigma&=\frac{N_1S_1+N_2S_2}{N} \end{align*} \]

Naive Bayesian

1. Model, 对单个数据点的各个维度作出限制
   \[ x_i\perp x_j|y,\forall\ i\ne j \]

   1. \(x_i\) 为连续变量：\(p(x_i|y)=\mathcal{N}(\mu_i,\sigma_i^2)\)
   2. \(x_i\) 为离散变量：类别分布（Categorical）：\(p(x_i=i|y)=\theta_i,\sum\limits_{i=1}^K\theta_i=1\)
   3. \(p(y)=\phi^y(1-\phi)^{1-y}\)

2. 解：和GDA相同

Dimension Reduction

中心化：
\[ \begin{align*}S &=\frac{1}{N}X^T(E_N-\frac{1}{N}\mathbb{I}_{N1}\mathbb{I}_{1N})(E_N-\frac{1}{N}\mathbb{I}_{N1}\mathbb{I}_{1N})^TX\\ &=\frac{1}{N}X^TH^2X=\frac{1}{N}X^THX \end{align*} \]

PCA

1. Idea: 坐标变换，寻找线性无关的新基矢，取信息损失最小的前几个维度

2. Loss Function:
   \[ \begin{align*}J &=\sum\limits_{j=1}^qu_j^TSu_j\ ,\ s.t.\ u_j^Tu_j=1 \end{align*} \]

3. 解：

   1. 特征分解法
      \[ S=U\Lambda U^T \]

   2. SVD for X/S
      \[ \begin{align*}HX=U\Sigma V^T\\ S=\frac{1}{N}V\Sigma^T\Sigma V^T \\new\ co=HX\cdot V\end{align*} \]

   3. SVD for T
      \[ \begin{align*}T=HXX^TH=U\Sigma\Sigma^TU^T\\ new\ co=U\Sigma \end{align*} \]

p-PCA

1. Model:
   \[ \begin{align*} z&\sim\mathcal{N}(\mathbb{O}_{q1},\mathbb{I}_{qq})\\ x&=Wz+\mu+\varepsilon\\ \varepsilon&\sim\mathcal{N}(0,\sigma^2\mathbb{I}_{pp}) \end{align*} \]

2. Learning: E-M

3. Inference:
   \[ p(z|x)=\mathcal{N}(W^T(WW^T+\sigma^2\mathbb{I})^{-1}(x-\mu),\mathbb{I}-W^T(WW^T+\sigma^2\mathbb{I})^{-1}W) \]

SVM

1. 强对偶关系：凸优化+（松弛）Slater 条件->强对偶。
2. 参数求解：KKT条件
   1. 可行域
   2. 互补松弛+梯度为0

Hard-margin

1. Idea: 最大化间隔

2. Model:
   \[ \mathop{argmin}_{w,b}\frac{1}{2}w^Tw\ s.t.\ y_i(w^Tx_i+b)\ge1,i=1,2,\cdots,N \]

3. 对偶问题
   \[ \max_{\lambda}-\frac{1}{2}\sum\limits_{i=1}^N\sum\limits_{j=1}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j+\sum\limits_{i=1}^N\lambda_i,\ s.t.\ \lambda_i\ge0 \]

4. 模型参数
   \[ \begin{gather*} \hat{w}=\sum\limits_{i=1}^N\lambda_iy_ix_i\\ \hat{b}=y_k-w^Tx_k=y_k-\sum\limits_{i=1}^N\lambda_iy_ix_i^Tx_k,\exists k,1-y_k(w^Tx_k+b)=0 \end{gather*} \]

Soft-margin

1. Idea:允许少量错误

2. Model:
   \[ \begin{gather*} error=\sum\limits_{i=1}^N\max\{0,1-y_i(w^Tx_i+b)\}\\ \mathop{argmin}_{w,b}\frac{1}{2}w^Tw+C\sum\limits_{i=1}^N\xi_i\ s.t.\ y_i(w^Tx_i+b)\ge1-\xi_i,\xi_i\ge0,i=1,2,\cdots,N \end{gather*} \]

Kernel

对称的正定函数都可以作为正定核。

Exp Family

1. 表达式
   \[ p(x|\eta)=h(x)\exp(\eta^T\phi(x)-A(\eta))=\frac{1}{\exp(A(\eta))}h(x)\exp(\eta^T\phi(x)) \]

2. 对数配分函数
   \[ \begin{align*} A'(\eta)=\mathbb{E}_{p(x|\eta)}[\phi(x)]\\ A''(\eta)=Var_{p(x|\eta)}[\phi(x)] \end{align*} \]

3. 指数族分布满足最大熵定理

PGM

Representation

1. 有向图
   \[ p(x_1,x_2,\cdots,x_p)=\prod\limits_{i=1}^pp(x_i|x_{parent(i)}) \]
   D-separation
   \[ p(x_i|x_{-i})=\frac{p(x)}{\int p(x)dx_{i}}=\frac{\prod\limits_{j=1}^pp(x_j|x_{parents(j)})}{\int\prod\limits_{j=1}^pp(x_j|x_{parents(j)})dx_i}=\frac{p(x_i|x_{parents(i)})p(x_{child(i)}|x_i)}{\int p(x_i|x_{parents(i)})p(x_{child(i)}|x_i)dx_i} \]

2. 无向图
   \[ \begin{align*}p(x)=\frac{1}{Z}\prod\limits_{i=1}^{K}\phi(x_{ci})\\ Z=\sum\limits_{x\in\mathcal{X}}\prod\limits_{i=1}^{K}\phi(x_{ci})\\ \phi(x_{ci})=\exp(-E(x_{ci})) \end{align*} \]

3. 有向转无向

   1. 将每个节点的父节点两两相连
   2. 将有向边替换为无向边

Learning

参数学习-EM

1. 目的：解决具有隐变量的混合模型的参数估计（极大似然估计）

2. 参数：
   \[ \theta_{MLE}=\mathop{argmax}\limits_\theta\log p(x|\theta) \]

3. 迭代求解：
   \[ \theta^{t+1}=\mathop{argmax}\limits_{\theta}\int_z\log [p(x,z|\theta)]p(z|x,\theta^t)dz=\mathbb{E}_{z|x,\theta^t}[\log p(x,z|\theta)] \]

4. 原理
   \[ \log p(x|\theta^t)\le\log p(x|\theta^{t+1}) \]

5. 广义EM

   1. E step：
      \[ \hat{q}^{t+1}(z)=\mathop{argmax}_q\int_zq^t(z)\log\frac{p(x,z|\theta)}{q^t(z)}dz,fixed\ \theta \]

   2. M step：
      \[ \hat{\theta}=\mathop{argmax}_\theta \int_zq^{t+1}(z)\log\frac{p(x,z|\theta)}{q^{t+1}(z)}dz,fixed\ \hat{q} \]

Inference

1. 精确推断

   1. VE

   2. BP
      \[ m_{j\to i}(i)=\sum\limits_j\phi_j(j)\phi_{ij}(ij)\prod\limits_{k\in Neighbour(j)-i}m_{k\to j}(j) \]

   3. MP
      \[ m_{j\to i}=\max\limits_{j}\phi_j\phi_{ij}\prod\limits_{k\in Neighbour(j)-i}m_{k\to j} \]

2. 近似推断

   1. 确定性近似，VI

      1. 变分表达式
         \[ \hat{q}(Z)=\mathop{argmax}_{q(Z)}L(q) \]

      2. 平均场近似下的 VI-坐标上升
         \[ \begin{gather*} \mathbb{E}_{\prod\limits_{i\ne j}q_i(Z_i)}[\log p(X,Z)]=\log \hat{p}(X,Z_j)\\ q_j(Z_j)=\hat{p}(X,Z_j) \end{gather*} \]

      3. SGVI-变成优化问题，重参数法
         \[ \begin{gather*} \mathop{argmax}_{q(Z)}L(q)=\mathop{argmax}_{\phi}L(\phi)\\ \nabla_\phi L(\phi)=\mathbb{E}_{q_\phi}[(\nabla_\phi\log q_\phi)(\log p_\theta(x^i,z)-\log q_\phi(z))]\\ =\mathbb{E}_{p(\varepsilon)}[\nabla_z[\log p_\theta(x^i,z)-\log q_\phi(z)]\nabla_\phi g_\phi(\varepsilon,x^i)]\\ z=g_\phi(\varepsilon,x^i),\varepsilon\sim p(\varepsilon) \end{gather*} \]

   2. 随机性近似

      1. 蒙特卡洛方法采样

         1. CDF 采样

         2. 拒绝采样， \(q(z)\)，使得 \(\forall z_i,Mq(z_i)\ge p(z_i)\)，拒绝因子：\(\alpha=\frac{p(z^i)}{Mq(z^i)}\le1\)

         3. 重要性采样
            \[ \mathbb{E}_{p(z)}[f(z)]=\int p(z)f(z)dz=\int \frac{p(z)}{q(z)}f(z)q(z)dz\simeq\frac{1}{N}\sum\limits_{i=1}^Nf(z_i)\frac{p(z_i)}{q(z_i)} \]

         4. 重要性重采样：重要性采样+重采样

      2. MCMC：构建马尔可夫链概率序列，使其收敛到平稳分布 \(p(z)\)。

         1. 转移矩阵（提议分布）
            \[ \begin{gather*} p(z)\cdot Q_{z\to z^*}\alpha(z,z^*)=p(z^*)\cdot Q_{z^*\to z}\alpha(z^*,z)\\ \alpha(z,z^*)=\min\{1,\frac{p(z^*)Q_{z^*\to z}}{p(z)Q_{z\to z^*}}\} \end{gather*} \]

         2. 算法（MH）：

            1. 通过在0，1之间均匀分布取点 \(u\)
            2. 生成 \(z^*\sim Q(z^*|z^{i-1})\)
            3. 计算 \(\alpha\) 值
            4. 如果 \(\alpha\ge u\)，则 \(z^i=z^*\)，否则 \(z^{i}=z^{i-1}\)

      3. Gibbs 采样：给定初始值 \(z_1^0,z_2^0,\cdots\)在 \(t+1\) 时刻，采样 \(z_i^{t+1}\sim p(z_i|z_{-i})\)，从第一个维度一个个采样。

GMM

1. Model
   \[ p(x)=\sum\limits_{k=1}^Kp_k\mathcal{N}(x|\mu_k,\Sigma_k) \]

2. 求解-EM
   \[ \begin{align*}Q(\theta,\theta^t)&=\sum\limits_z[\log\prod\limits_{i=1}^Np(x_i,z_i|\theta)]\prod \limits_{i=1}^Np(z_i|x_i,\theta^t)\\ &=\sum\limits_z[\sum\limits_{i=1}^N\log p(x_i,z_i|\theta)]\prod \limits_{i=1}^Np(z_i|x_i,\theta^t)\\ &=\sum\limits_{i=1}^N\sum\limits_{z_i}\log p(x_i,z_i|\theta)p(z_i|x_i,\theta^t)\\ &=\sum\limits_{i=1}^N\sum\limits_{z_i}\log p_{z_i}\mathcal{N(x_i|\mu_{z_i},\Sigma_{z_i})}\frac{p_{z_i}^t\mathcal{N}(x_i|\mu_{z_i}^t,\Sigma_{z_i}^t)}{\sum\limits_kp_k^t\mathcal{N}(x_i|\mu_k^t,\Sigma_k^t)} \end{align*} \]

   \[ p_k^{t+1}=\frac{1}{N}\sum\limits_{i=1}^Np(z_i=k|x_i,\theta^t) \]

序列模型-HMM，LDS，Particle

1. 假设：

   1. 齐次 Markov 假设（未来只依赖于当前）：
      \[ p(i_{t+1}|i_t,i_{t-1},\cdots,i_1,o_t,o_{t-1},\cdots,o_1)=p(i_{t+1}|i_t) \]

   2. 观测独立假设：
      \[ p(o_t|i_t,i_{t-1},\cdots,i_1,o_{t-1},\cdots,o_1)=p(o_t|i_t) \]

2. 参数
   \[ \lambda=(\pi,A,B) \]

离散线性隐变量-HMM

1. Evaluation：\(p(O|\lambda)\)，Forward-Backward 算法
   \[ \begin{gather*} p(O|\lambda)=\sum\limits_{i=1}^Np(O,i_T=q_i|\lambda)=\sum\limits_{i=1}^N\alpha_T(i)=\sum\limits_{i=1}^Nb_i(o_1)\pi_i\beta_1(i)\\ \alpha_{t+1}(j)=\sum\limits_{i=1}^Nb_{j}(o_t)a_{ij}\alpha_t(i)\\ \beta_t(i)=\sum\limits_{j=1}^Nb_j(o_{t+1})a_{ij}\beta_{t+1}(j) \end{gather*} \]

2. Learning：\(\lambda=\mathop{argmax}\limits_{\lambda}p(O|\lambda)\)，EM 算法（Baum-Welch）
   \[ \begin{align*} \lambda^{t+1}&=\mathop{argmax}_\lambda\sum\limits_I\log p(O,I|\lambda)p(O,I|\lambda^t)\\&=\sum\limits_I[\log \pi_{i_1}+\sum\limits_{t=2}^T\log a_{i_{t-1},i_t}+\sum\limits_{t=1}^T\log b_{i_t}(o_t)]p(O,I|\lambda^t) \end{align*} \]

3. Decoding：\(I=\mathop{argmax}\limits_{I}p(I|O,\lambda)\)，Viterbi 算法-动态规划
   \[ \begin{gather*} \delta_{t}(j)=\max\limits_{i_1,\cdots,i_{t-1}}p(o_1,\cdots,o_t,i_1,\cdots,i_{t-1},i_t=q_i)\\\delta_{t+1}(j)=\max\limits_{1\le i\le N}\delta_t(i)a_{ij}b_j(o_{t+1})\\\psi_{t+1}(j)=\mathop{argmax}\limits_{1\le i\le N}\delta_t(i)a_{ij} \end{gather*} \]

连续线性隐变量-LDS

1. Model
   \[ \begin{align*} p(z_t|z_{t-1})&\sim\mathcal{N}(A\cdot z_{t-1}+B,Q)\\ p(x_t|z_t)&\sim\mathcal{N}(C\cdot z_t+D,R)\\ z_1&\sim\mathcal{N}(\mu_1,\Sigma_1) \end{align*} \]

2. 滤波
   \[ \begin{align*} p(z_t|x_{1:t})&=p(x_{1:t},z_t)/p(x_{1:t})\propto p(x_{1:t},z_t)\\&=p(x_t|z_t)p(z_t|x_{1:t-1})p(x_{1:t-1})\propto p(x_t|z_t)p(z_t|x_{1:t-1}) \end{align*} \]

3. 递推求解-线性高斯模型

   1. Prediction
      \[ \begin{align*} p(z_t|x_{1:t-1})&=\int_{z_{t-1}}p(z_t|z_{t-1})p(z_{t-1}|x_{1:t-1})dz_{t-1}\\&=\int_{z_{t-1}}\mathcal{N}(Az_{t-1}+B,Q)\mathcal{N}(\mu_{t-1},\Sigma_{t-1})dz_{t-1} \end{align*} \]

   2. Update:
      \[ p(z_t|x_{1:t})\propto p(x_t|z_t)p(z_t|x_{1:t-1} \]

连续非线性隐变量-粒子滤波

通过采样(SIR)解决：
\[ \mathbb{E}[f(z)]=\int_zf(z)p(z)dz=\int_zf(z)\frac{p(z)}{q(z)}q(z)dz=\sum\limits_{i=1}^Nf(z_i)\frac{p(z_i)}{q(z_i)} \]

1. 采样
   \[ \begin{gather*} w_t^i\propto\frac{p(x_t|z_t)p(z_t|z_{t-1})}{q(z_t|z_{1:t-1},x_{1:t})}w_{t-1}^i\\ q(z_t|z_{1:t-1},x_{1:t})=p(z_t|z_{t-1}) \end{gather*} \]

2. 重采样

CRF

1. PDF
   \[ p(Y=y|X=x)=\frac{1}{Z(x,\theta)}\exp[\theta^TH(y_t,y_{t-1},x)] \]

2. 边缘概率
   \[ \begin{gather*} p(y_t=i|x)=\sum\limits_{y_{1:t-1}}\sum\limits_{y_{t+1:T}}\frac{1}{Z}\prod\limits_{t'=1}^T\phi_{t'}(y_{t'-1},y_{t'},x)\\ p(y_t=i|x)=\frac{1}{Z}\Delta_l\Delta_r\\ \Delta_l=\sum\limits_{y_{1:t-1}}\phi_{1}(y_0,y_1,x)\phi_2(y_1,y_2,x)\cdots\phi_{t-1}(y_{t-2},y_{t-1},x)\phi_t(y_{t-1},y_t=i,x)\\ \Delta_r=\sum\limits_{y_{t+1:T}}\phi_{t+1}(y_t=i,y_{t+1},x)\phi_{t+2}(y_{t+1},y_{t+2},x)\cdots\phi_T(y_{T-1},y_T,x) \end{gather*} \]

   \[ \begin{gather*} \alpha_t(i)=\Delta_l=\sum\limits_{j\in S}\phi_t(y_{t-1}=j,y_t=i,x)\alpha_{t-1}(j)\\ \Delta_r=\beta_t(i)=\sum\limits_{j\in S}\phi_{t+1}(y_t=i,y_{t+1}=j,x)\beta_{t+1}(j) \end{gather*} \]

3. 学习
   \[ \nabla_\lambda L=\sum\limits_{i=1}^N\sum\limits_{t=1}^T[f(y_{t-1},y_t,x^i)-\sum\limits_{y_{t-1}}\sum\limits_{y_t}p(y_{t-1},y_t|x^i)f(y_{t-1},y_t,x^i)] \]